In an induction motor, for fast dynamic electromagnetic torque response, it is preferable to maintain the air-gap flux at rated value. This is achieved in V/f control, where the ratio of applied terminal voltage to that of its frequency is held a constant equal to the value at rated condition. The speed of the motor is controlled by adjusting the applied frequency while maintaining V/f constant. This experiment deals with how to design a closed loop V/f speed controller for an induction motor.
Small signal motor model
From the Sprevious experiment, the per-phase equivalent model of an induction motor is as shown below, containing both the electrical and mechanical model:
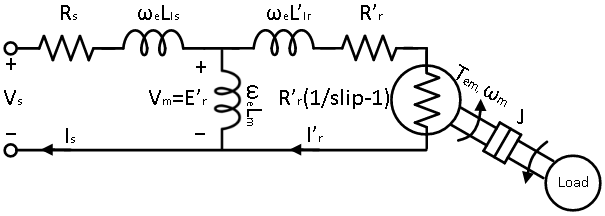
In the above steady-state per-phase equivalent circuit, the s terms have been replaced by the complex variable jω. This is justified by the fact that the electrical time constant of practical induction motors are orders of magnitude lower than that of the mechanical time constant. Thus, while designing a controller to control the motor's mechanical rotational speed, the transients associated with the electromagnetic circuit of the motor can be reasonably ignored. Hence, the per-phase steady state equivalent circuit can be assumed to be a good enough model to derive the motor's non-mechanical transfer function.
The flux in the air-gap is a function of the current flowing through the magnetizing inductance Lm, which is given in Eqn. 1. If the drop across the stator resistance Rs and stator leakage inductance Lls is ignored, the voltage across the magnetizing inductance Vm equals the applied terminal voltage Vs as given in Eqn 2.
Φ ∝ Im = VmjωeLm(1)
Im ≈ VsjωeLm(2)
where, ωe = 2πf, f is the frequency (in Hz) of the applied terminal voltage. ωe is related to the slip as given by:
ωe = P2 × ωsync = P2 × (ωmech + ωslip) = P2 × (ωmech + slip × ωsync) (3)
For fast dynamic response, the flux is maintained at rated value for most of the operating region of the induction motor. Maintaining it higher than the rated value will lead to core saturation, leading to increased losses and harmonics. Maintaining it lower than the rated value will lead to increased rotor losses, as well as limits the maximum continuous torque that can be generated. So, under most operating conditions, the applied terminal voltage can be expressed as function of applied frequency:
Vs ≈ Vs, ratedωe, rated × ωe = C × ωe(4)
where, Vs, rated and ωe, rated are the rated per-phase terminal voltage and frequency.
The motor speed is controlled by controlling the frequency of the applied voltage. This is achieved by using a PI controller. To tune this controller for desired performance, the system transfer function needs to be established that links the applied frequency to the rotor speed, which is done in the following section.
The mechanical model of the Induction motor is given in Eqn. 5. Under steady state condition, the torque generated by the motor Tem equals the sum of load torque Tl and the torque necessary to compensate the frictional losses, Tfric. In transient condition when Tem ≠ Tl + Tfric, the motor accelerates if the former is greater than the latter, storing the excess energy as inertial energy. It decelerates if the former is less than the latter, loosing previously stored inertial energy. The motor inertia is identified as J in Eqn. 5, where ωm is the mechanical rotor speed.
Tem = Tl + Tfric + Jdωmdt(5)
The frictional component occurs due to various factors and is always against the direction of rotation. Of the many causes, only Coulomb friction which is a constant and viscous friction which varies proportionately with rotational speed are considered, since these are the ones that have significant effect on the steady-state. The torque associated with Coulomb friction is given by Tc and that of viscous friction is given by B × ωm, where B is the coefficient of viscous friction. Substituting these into Eqn. 5 yields the final mechanical model as given in Eqn. 6.
Tem = Tl + Tc + Bωm + Jdωmdt(6)
which can be expressed in transfer function form as:
ωm(s)Tem(s) - Tl(s) = 1sJ + B(7)
From above equation, under constant load condition, a small incremental perturbation in electromagnetic torque ΔTem leads to incremental change in rotor speed Δωm:
Δωm(s) = ΔTem(s)sJ + B(8)
Having established the small signal relationship between Tem and ωm, relationship between Tem and applied frequency must be established, to complete the system model. From the equivalent circuit, the output power of an induction motor is as given in Eqn. 9. This is same as the product of the electromagnetic torque and the motor speed.
Pout = 3 × I'r2 × R'r × 1 - slipslip(9)
Tem = Poutωm = Pout(1 - slip) × ωsync = 3 × I'r2 × R'rslip × ωsync(10)
where, ωsync = 2Pωe, P is the number of poles.
The reflected rotor current transfer function I'r(s) in the above equation equals:
I'r(s) = Vs(s)Zs(s) + Zm(s)Zr(s)Zm(s) + Zr(s) × Zm(s)Zm(s) + Zr(s)(11)
where,
Zs(s) = Rs + sLls(12)
Zr(s) = R'rslip + sLlr(13)
Zm(s) = sLm(14)
Under rated load condition, Zm is much greater than Zr, leading to the above equation being simplified to Eqn. 15. Under light load condition, Zr is much greater than Zm and Zs, leading to above equation being simplified to Eqn. 16. To keep the method for PI tuning same across the region of operation, for the sake of simplicity, Zs is added to the denominator of Eqn. 16 to make it same as Eqn. 15. This shouldn't have any noticeable effect on the operation since at the light load condition, Zs is much less than Zr. These approximations do not alter the performance significantly but reduces the order of the rotor current to applied stator voltage transfer function, leading to much simpler design.
I'r(s) ≈ Vs(s)Zs(s) + Zr(s)(15)
I'r(s) ≈ Vs(s)Zr(s)(16)
Substituting this approximation into Eqn. 10 yields Eqn. 17.
Tem(slip) = 3 × Vs2slip × ωsync × R'r|Zs(s) + Zr(s)|2(17)
Since Vs/ωsync is constant C in this scenario, above equation becomes:
Tem(slip) = 3C2ωsyncslip × R'r|Zs(s) + Zr(s)|2 = 3C2ωsyncslip × R'r|Rs + R'rslip + jωe(Lls + Llr)|2(18)
⇒ Tem(slip) = 3C2ωsyncR'r × slip|slip × (Rs + jωe(Lls + Llr)) + R'r|2(19)
The above system is linearized around the rated operating condition. From above equation, under operating slip slipop, a small incremental perturbation in slip, Δslip leads to inremental change in electromagnetic torque ΔTem:
∂Tem∂slip = 3C2ωsyncR'r × R'r2 - (slipopR)2((slipopR)2 + 2slipopRsRr + R'r2)2(20)
∂Tem∂slip = kt(21)
where,
R2 = Rs2 + (ωeLls + ωeLlr)2(22)
PI Controller design
The overall transfer function is shown below, including the PI controller:
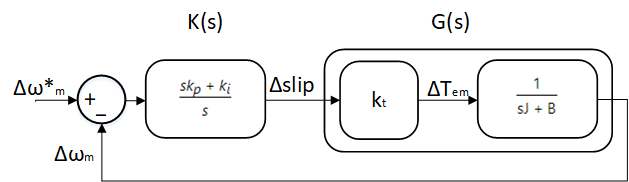
The overall open loop transfer function is:
Δωm(s)Δslip(s) = Δωm(s)ΔTem(s)×ΔTem(s)Δslip(s) = ks,ps + ks,is × ktJs + B(23)
Now, the kp and ki are chosen such that the cross over frequency ω of the above transfer function is ωc with a phase margin Φ = Φc. At the cross over frequency, the above transfer function has a magnitude of 1 and phase angle of -π + Φc. This yields the following equation:
ks,p = C2 × ks,i(24)
where,
C2 = 1ωs,c × tan(Φs - π2 + tan-1(ωs,cJB))(25)
and
k2s,i= (ωs,ckt)2 × (ωs,cJ)2 + B2(ωs,c × C2)2 + 1(26)
Region of operation
Figure below shows the region of operation, i.e. the applied stator voltage as function of frequency.
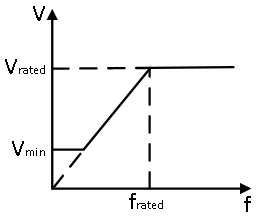
The above system design was carried out in the linear region. At low frequencies, the approximation Vm ≈ Vs fails because the drop across stator resistance is significant compared to drop across magnetizing inductance. Due to this applying the constant V/f used in the linear region will not generate sufficient flux and as a consequence the electromagnetic torque is limited. To avoid this, at low frequencies, a constant minimum voltage is applied, until the linear region is entered.
At frequencies higher than the rated, the V/f ratio can no longer be maintained due to:
Exceeding rated voltage could cause motor insulation failure.
The available DC bus voltage is limited, hence the 3Φ inverter output voltage is limited.
Due to these limitations, at above the rated frequency, the voltage is maintained at rated while frequency is increased. This leads to reduced maximum torque due to reduced air-gap flux. This is called field weakening, where compromise is made on maximum electromagnetic torque to achieve higher speeds.
In the following section, a pre-built closed loop speed control model is run in both simulation and real-time.
Open Workbench and pin the Explorer and Properties dock.
Navigate to and open the IMabc project file in Experiment3\Simulation folder usually in the following location: C:\Program Files (x86)\Sciamble\WorkBench v1\Examples\CUSPLab\AdvancedDrives.
Expand the project in the Explorer and open the IMabcModel model file shown below:
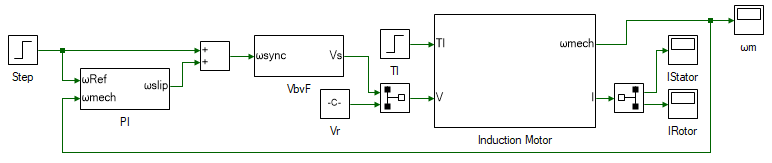
At the center of the model is the linearized mathematical model of an induction motor. The system is modeled in abc domain and details of the design is not dealt in this experiment. The same model is developed as part of next experiment in dq domain. The inputs to the motor model are 3Φ stator voltage and load torque. Based on the inputs, the model computes and outputs the 3Φ stator and rotor current, and the rotor mechanical rotational speed. The load torque is simulated with a step of 0.05 Nm applied at 3 s. The 3Φ rotor voltages are set to 0 since the motor under consideration is a squirrel-cage induction motor, whose rotor is shorted. The 3Φ stator voltage is computed based on the desired input voltage frequency, inside the VbyF subsystem, using the V/f control discussed earlier.
The desired input voltage frequency is in turn determined by the closed loop speed controller. Based on the error between the desired speed and the actual speed, the desired slip speed ωslip is determined by the PI controller. The frequency of the applied terminal stator voltage is determined by Eqn. 3, based on the desired rotor speed ωmech and required slip speed ωslip to achieve the desired rotor speed.
Open the IMParam script, within the project file in the Explorer. A section of the file shown below:
Update the motor parameter values in the script file to the values determined in the previous experiment.
The script file consists of the function CalcKpKi() which computes the speed controller's kp and ki gains based on the motor parameters, and the controller phase margin and cross-over frequency. This is done based on Eqns. 3 through 25. This function must be called prior to running the simulation model to initialize the controller gain values. To do this open project properties, double click on the IMabc project node in the Explorer, and set the Prerun Model/Function to IMParam:CalcKpKi() as shown below:
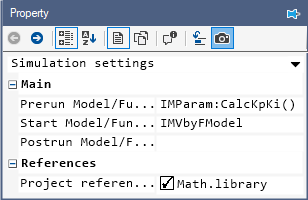
The cross-over frequency ωc is set to 50 rads/s and the phase margin φc is set to 60° in the script file.
Similarly set the Start model/Function to IMabcModel which is the V/f control model discussed earlier.
NoteThe value set here is the model-name which is not always as model's file name. The model-name can be different from the file name displayed in the Explorer tab. The model name is present in model's property which can be viewed by double clicking anywhere on the blank space in the model file.
Click the 
button to run the model.
Observe the motor speed response to a step change in reference speed at time 1 s and a step change in load torque at time 3s.
Make note of the kp and ki values. To do this, open the PI subsystem in the IMabcModel. Select the gain block labelled kp. Open the DataPeek dock on the right and select the
button in the dock's toolbar to view the data of selected tool. The tool's gain value will be displayed as shown below:
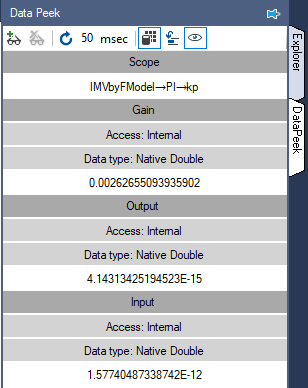
Similarly, select the tool labelled ki to look at the value of the integrator gain. The DataPeek can be used in a similar manner to view the runtime data of any tool.
Rerun the simulation for the following cross-over frequency: 20 rad/s, 100 rads/s and 150 rads/s and phase margin of 30, 60 and 90 degrees. Observe the speed and current response for each of those value.
It must be noted that the controller performs as expected only in and around the rated operating condition since the induction motor model was linearized in Eqn. 20 around this operating point. Also, during the derivation of the system equation, a major simplifying assumption was made, that the time constant of the mechanical system is much higher than that of the electrical system. This justified the use of the steady-state electrical per-phase equivalent motor model to derive the system transfer function. This assumption becomes increasingly invalid as the cross-over frequency/bandwidth of the speed control loop increases.
In the following section, the V/f closed loop speed control in real-time to control the induction motor speed and to observe the motor speed and current response under different load conditions and controller parameters.
Open a new Workbench session.
Create a new project and add a model file to it. Set this model file as the Start model/Function in project properties.
Open model properties and set the Step time to 0.0001 and the Run time to 5.
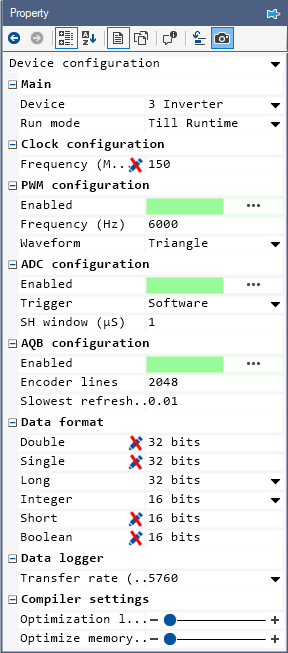
Within the project properties, select the drop-down menu on the top and select Device Configuration. Within this, change the following properties:
Change Device within Main sub-division to 3 Inverter
Change Run mode within Main sub-division to Till Runtime.
Change Waveform within PWM configuration sub-division to Triangle.
Change Encoder lines within AQB configuration sub-division to 2048.
Change Transfer rate within Data logger sub-division to 5760.
The overall model to do real-time induction motor V/f speed control is shown below and this will be built in the following steps.
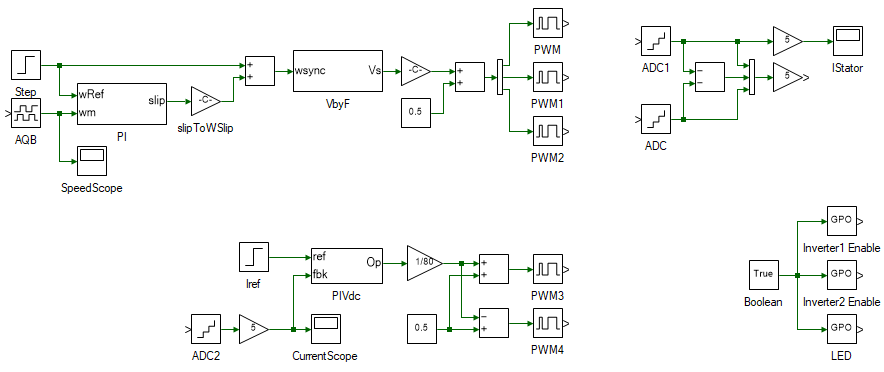
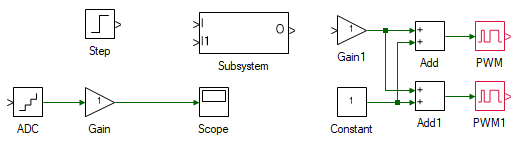
To load the induction motor, a DC generator is used similar to the previous experiment. This is done by the tools in the bottom left in the above overall model. To build the same, drag and drop the following tools from the Toolbox to the model and connect them as shown.
| # | Tool type | Tool class | Tool name |
|---|---|---|---|
| 1 | Step | Signal Sources | Step |
| 2 | Analog Input | Hardware Integration | ADC |
| 3 | Gain | Math Block | Gain |
| 4 | Mag-Time Scope | Display | Scope |
| 5 | Subsystem | Signal Routing | Subsystem |
| 6 | Gain | Math Block | Gain1 |
| 7 | Constant | Signal Sources | Constant |
| 8 | Adder Subtractor | Math Block | Add |
| 9 | Adder Subtractor | Math Block | Add1 |
| 10 | PWM Output | Hardware Integration | PWM |
| 11 | PWM Output | Hardware Integration | PWM1 |
While adding these tools, some of them might be highlighted in red. If the model has any such errors, the button is disabled till these errors are fixed. To look at the cause of these errors,
open the Messages tab in the bottom and select the Errors options. Clicking on those errors takes the view to the source of the errors. These errors will be fixed in the following steps.
In the above system, the Step tool represents the desired DC generator current, in turn, the load torque. This is compared with the actual DC generator current as read by the ADC tool. Within the subsystem, the PI controller to control the applied terminal voltage to generate the desired current is designed. The output of the subsystem will be the terminal voltage. This is converted to PWM duty-cycles between 0-1 in the following blocks.
Open the subsystem, by double clicking on it, to design the PI controller. Drag and drop the following tools and connect them as shown:
| # | Tool type | Tool class | Tool name |
|---|---|---|---|
| 1 | In-port | Signal Routing | I |
| 2 | In-port | Signal Routing | I1 |
| 3 | Adder Subtractor | Math Block | Add |
| 4 | Gain | Math Block | Gain |
| 5 | Gain | Math Block | Gain1 |
| 6 | Integrator | Math Block | Integrator |
| 7 | Adder Subtractor | Math Block | Add1 |
| 8 | Saturation | Non-linear | Saturation |
| 9 | Out-port | Signal Routing | O |
Change the properties of each tool within the subsystem to values listed in table below.
| Tool name | Property field | Property value | Comments |
|---|---|---|---|
| I | Name | ref | PI controller reference. |
| I1 | Name | fbk | PI controller feedback. |
| Add | Arithmetic operation | +- | Difference between the reference and feedback. |
| Gain | Gain | 0.6132 | DC motor PI current controller's proportional gain. |
| Gain1 | Gain | 250 | DC motor PI current controller's integral gain. |
| Integrator | Integrator type | Anti-windup | This prevents the integrator from building up to a very large value due to real-world saturation. |
| Integrator | Upper limit | 15 | Limited to the maximum voltage to be outputed to the DC generator. |
| Integrator | Lower limit | -15 | Limited to the minimum voltage to be outputed to the DC generator. |
| Saturation | Upper limit | 15 | Limited to the maximum voltage to be outputed to the DC generator. |
| Saturation | Lower limit | -15 | Limited to the minimum voltage to be outputed to the DC generator. |
| O | Name | Op | PI controller output. This is terminal voltage applied to the DC generator. |
Change the properties of each tool outside the subsystem to values listed in table below.
| Tool name | Property field | Property value | Comments |
|---|---|---|---|
| Step | Final value | 0.5 | 0.5 A step change in DC generator current. This translates to 0.05 Nm for the DC generator used. |
| Step | Step time | 3 | Step the load at time 3 s. |
| ADC | Channel | 5 | Phase-A current of Inverter 2, to which the DC generator is connected. |
| Gain | Gain | 5 | Scaling to convert ADC signal to actual current. The scaling value is given within the ADC property. |
| Gain1 | Gain | 1/80 | 1/(2 x Vdc) to convert the voltage to a value between ±0.5. |
| Constant | Magnitude | 0.5 | Above signal is centered around 0.5 to get the duty cycle. |
| Add1 | Arithmetic operation | -+ | Duty cycle of one of the inverter leg is obtained by adding the scaled duty to 0.5 and other by subtracting it from 0.5. |
| PWM | Channel | 4 | Each PWM channel controls the voltage across one of the output terminals. |
| PWM1 | Channel | 5 | Each PWM channel controls the voltage across one of the output terminals. |
Complete the remaining connections to as shown:
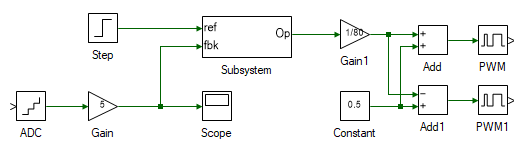
This completes the real-time design to emulate a step change in load torque.
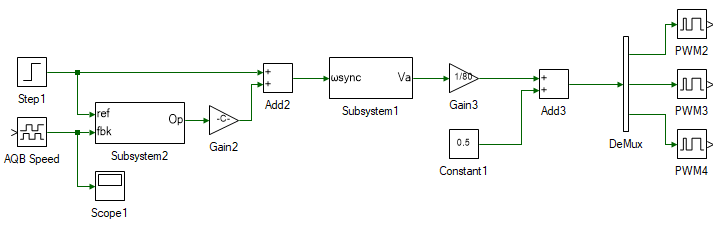
In the following steps, a closed loop V/f speed controller is designed. This is done by the tools in the top left in the overall model seen earlier. To build the same, drag and drop the following tools as shown:
| # | Tool type | Tool class | Tool name |
|---|---|---|---|
| 1 | Step1 | Signal Sources | Step |
| 2 | AQB Speed | Hardware Integration | AQB Speed |
| 3 | Mag-Time Scope | Display | Scope1 |
| 4 | Gain | Math Block | Gain2 |
| 5 | Adder Subtractor | Math Block | Add2 |
| 6 | Subsystem | Signal Routing | Subsystem1 |
| 7 | Gain | Math Block | Gain3 |
| 8 | Constant | Signal Sources | Constant1 |
| 9 | Adder Subtractor | Math Block | Add3 |
| 10 | DeMux | Signal Routing | DeMux |
| 11 | PWM Output | Hardware Peripherals | PWM2 |
| 12 | PWM Output | Hardware Integration | PWM3 |
| 13 | PWM Output | Hardware Integration | PWM4 |
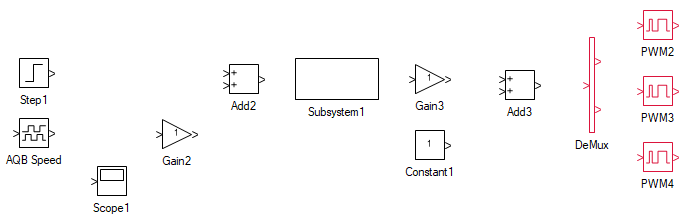
The speed controller used is the same PI controller as the one used for DC generator current controller which was designed previous steps. Copy paste (select the subsystem, CtrlC, CtrlV) the PI controller subsystem designed earlier as shown:
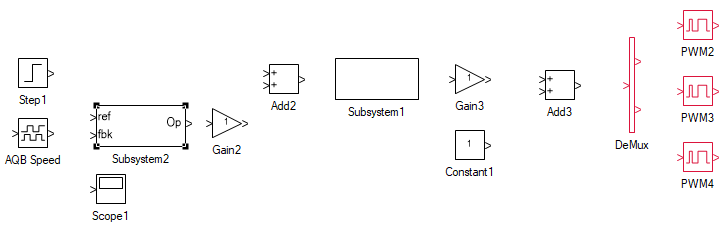
In the above system, the Step1 tool represents the desired Induction motor speed. This is compared with the actual induction motor speed as read by the AQB Speed tool. The output of the PI subsystem is the slip speed required to generated the desired steady-state motor speed. This is added to the desired motor speed to get the frequency of applied motor terminal voltage. This is followed by the subsystem which will contain the V/f logic and outputs the 3Φ induction motor terminal voltage. This is converted to PWM duty-cycles between 0-1 in the following blocks. The Sine-PWM modulation is used here.
Within the copy-pasted subsystem, set the following properties:
| Tool name | Property field | Property value | Comments |
|---|---|---|---|
| Gain | Gain | kp noted from simulation for cross-over frequency of 50 rads/s and phase margin of 60°. | Induction motor PI speed controller's proportional gain. |
| Gain1 | Gain | ki noted from simulation for cross-over frequency of 50 rads/s and phase margin of 60°. | Induction motor PI speed controller's integral gain. |
| Integrator | Integrator type | Anti-windup | This prevents the integrator from building up to a very large value due to real-world saturation. |
| Integrator | Upper limit | 0.1 | Limited to the maximum slip of the induction motor. |
| Integrator | Lower limit | -0.1 | Limited to the minimum slip of the induction motor. |
| Saturation | Upper limit | 0.1 | Limited to the maximum slip of the induction motor. |
| Saturation | Lower limit | -0.1 | Limited to the minimum slip of the induction motor. |
Open the V/f subsystem, the one labelled Subsystem1. Drag and drop the following tools and connect them as shown:
| # | Tool type | Tool class | Tool name |
|---|---|---|---|
| 1 | In-port | Signal Routing | I |
| 2 | Gain | Math Block | Gain |
| 3 | Gain | Math Block | Gain1 |
| 4 | Integrator | Math Block | Integrator |
| 5 | Increment | Math Block | Increment |
| 6 | Elementary Function | Math Block | Elementary Fnc |
| 7 | Multiplier Divider | Math Block | Multiply |
| 8 | Out-port | Signal Routing | O |
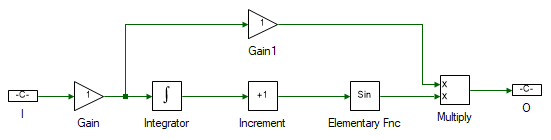
Change the properties of each tool within the subsystem to values listed in table below.
| Tool name | Property field | Property value | Comments |
|---|---|---|---|
| I | Name | ωsync | Synchronous speed. |
| Gain | Gain | 2 | Scaled by Pole-pairs/2 to convert synchronous speed to terminal voltage's frequency. The motor has 4 pole-pairs. |
| Integrator | - | No change | Integrate the frequency to obtain the angle of the terminal voltge. |
| Gain1 | Gain | 0.06238 | Scale frequency by Vph-peak,rated/2πfrated ratio to get the magnitude of the applied 3Φ terminal voltage. The motor is rated for 24V line-line rms and 50Hz. |
| Increment | Offset | {0, -2*π/3, -4*π/3} | Offset the angle by 2π/3 and 4π/3 to get the angle of voltages of all the three phases. |
| O | Name | Va | Applied 3Φ terminal voltage. |
The remaning blocks, namely the Elementary Fnc and Multiply computes the 3Φ terminal voltage based on the angle and the magnitude.
Change the properties of each tool outside the subsystem to values listed in table below.
| Tool name | Property field | Property value | Comments |
|---|---|---|---|
| Step | Final value | 100 | Induction motor reference speed of 100 rads/s. |
| Step | Step time | 1 | Step the reference at time 1 s. |
| AQB Speed | Channel | 1 | This is the DSUB port to which the encoder is connected to. |
| Scope | Realtime log | Enabled | By default, scope only logs data in simulation. To log in real-time as well, it must be enabled. |
| Gain2 | Gain | 157.08 | 2πfrated/(2 x P) to convert slip to ωslip. |
| Gain3 | Gain | 1/80 | 1/(2 x Vdc) to convert the voltage to a value between ±0.5. |
| Constant | Magnitude | 0.5 | Above signal is centered around 0.5 to get the duty cycle. |
| DeMux | Number of ports | 3 | Split the muxed 3Φ duty-cycle to individual phases. |
| PWM2 | Channel | 1 | Phase-A. |
| PWM3 | Channel | 2 | Phase-B. |
| PWM4 | Channel | 3 | Phase-C. |
NoteUse scopes in real-time mode judiciously. There is limited bandwidth for real-time data logging and more the number of scopes, which log data in real-time, proportionally lower is the sample rate of each. To observe slow varying signals, consider using other tools in the Display toolbox. These tools, relative to Scope, logs slowly at around every 200 ms. Hence, these do not consume much bandwidth.
Connect the tools as shown:
This completes the V/f closed loop induction motor speed controller design.
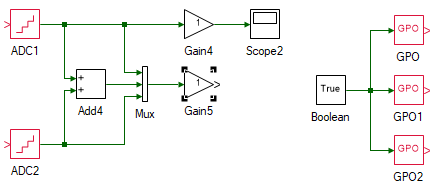
The final remaining components of the overall model is the current measurement on the top right and the inverter enable at the bottom right. Add the following tools and connect them as shown:
| # | Tool type | Tool class | Tool name |
|---|---|---|---|
| 1 | Analog Input | Hardware Integration | ADC1 |
| 2 | Analog Input | Hardware Integration | ADC2 |
| 3 | Adder Subtractor | Math Block | Add4 |
| 4 | Mux | Signal Routing | Mux |
| 5 | Gain | Math Block | Gain4 |
| 6 | Gain | Math Block | Gain5 |
| 7 | Mag-Time Scope | Display | Scope |
| 8 | True/False | Signal Sources | Boolean |
| 9 | Digital Output | Hardware Integration | GPO |
| 10 | Digital Output | Hardware Integration | GPO1 |
| 11 | Digital Output | Hardware Integration | GPO2 |
Set the properties of the above tools as given:
| Tool name | Property field | Property value | Comments |
|---|---|---|---|
| ADC1 | Channel | 3 | Inverter 1's/induction motor's phase-A current. |
| ADC2 | Channel | 4 | Inverter 1's/induction motor's phase-C current. |
| Add4 | Arithmetic operation | -- | Difference of phase-A and phase-C current to obtain phase-B current. |
| Mux | Number of ports | 3 | Mux the 3Φ currents. |
| Gain4 | Gain | 5 | Scaling to convert ADC signal to actual current. The scaling value is given within the ADC property. |
| Gain5 | Gain | 5 | Scaling to convert ADC signal to actual current. The scaling value is given within the ADC property. |
| Scope2 | Realtime log | Enabled | This scope is connected to measure only phase-A current. This can instead be connected to Gain4 to measure the 3Φ currents but the data logger does not have sufficient bandwidth to display three 50 Hz signals at the same time with sufficient resolution. |
| Boolean | No change | Set to true to enable the inverter modules. | |
| GPO | Channel | 1 | Enable inverter 1 which is connected to the induction motor. |
| GPO1 | Channel | 2 | Enable inverter 2 which is connected to the DC generator. |
| GPO2 | Channel | 4 | Green LED on the side of the ThreeInverter module, just to indicate when the model is running in real-time. |
This completes the model for real-time closed loop V/f speed control of induction motor.
Turn ON the DC power supply and set the voltage to 40 V.
Ensure that 
button on the top dock, to transition to real-time mode, is pressed. Click the run button.
Observe the speed and current result in the scope. Click the 
to focus the result. After about 5 s, stop data logging by clicking 
.
NoteIf the motor fails to reach the reference speed, scale the V/f ratio (Step 15) by a factor of 1.3. Repeat this step once more if necessary. Do not set V/f ratio any greater that twice the rated value computed in Step 15.
Turn OFF the DC power supply.
If necessary, repeat the experiment for different controller gain values.
Turn OFF the DC power supply and disconnect all the connections including the USB.
List the kp and ki values for the three different cross-over frequency and phase margins. Compare if they are same as the values calculated by hand using Eqns. 3 through 35.
Attach the plot of motor speed and 3Φ current response from simulation for the three different cross-over frequency and phase margins. Comment on the differences in the response and the reason.
Attach the plot of motor speed and phase-A current response from real-time.
If the motor is expected to perform as desired while operating at half its rating, how would the system be redesigned?
Read through and add comments to each line of code in the CalcKpKi() function. Later experiments would require writing the script file to compute the controller parameters.
