Vector control of PMSM

August 03, 2019
3 hours to complete
Workbench v1.5

Introduction

In this experiment, a dq model of a surface permanent magnet AC (PMAC) motor will be simulated. The speed of the PMAC motor will be controlled using a closed loop PI controller which will be designed in this experiment. In addition to simulation, the controller designed will also be evaluated on an actual PMAC motor in real-time.

Theoretical background

Motor model

The following set of equations represents a linearized surface PMAC motor in the dq frame with the d-axis aligned with the rotor magnetic flux axis [1]:

v_sd = R_si_sd - ω_mλ_sq + dλ_sddt(1)

v_sq = R_si_sq + ω_mλ_sd + dλ_sqdt(2)

λ_sd = L_si_sd + λ_fd(3)

λ_sq = L_si_sq(4)

T_em = P2λ_fdi_sq = k_ti_sq(5)

T_em = T_l + Jdω_mechdt + Bω_mech(6)

ω_m = P2ω_mech(7)

where

V_sd, V_sq : stator d and q axis voltage respectively
I_sd, I_sq : stator d and q axis current respectively
λ_fd : stator flux-linkage due to rotor magnets
R_s : stator resistance
L_s : L_ls + L_m where, L_ls is the stator leakage inductance and L_m per-phase mutual inductance
J : rotor inertia
B : coefficient of viscous friction
P : Number of stator poles
T_em : output/electromagnetic torque
T_l : load torque
ω_mech : rotor mechanical speed
ω_m : d-axis rotational speed

Current controller design

Unlike an induction motor where the flux is established through stator currents, in case of PMAC motor, the flux is established by the rotor magnets. Hence, under normal operating conditions, the d-axis current i_d is maintained at zero. Applying a positive i_d will cause the net air-gap flux magnitude to reduce due to the opposing direction the stator d-axis current induced flux and the rotor magnet flux along which the d-axis is aligned. The electromagnetic torque is adjusted by controlling the stator q-axis current. The desired stator dq currents are synthesized by the controlling the applied stator dq voltages by means of a PI controller. The PI controller's gain values are determined as done in earlier experiments by defining the desired transient response of the system in terms of cross-over frequency and phase margin.

To design the current PI controller, Eqns. 3 and 4 are substituted into Eqns. 1 and 2, and are rewritten in the following form:

v_sd = R_si_sd + L_sdi_sddt - ω_mL's'i_sq(8)

v_sq = R_si_sq + L_sdi_sqdt + ω_m(L_mi_sd + λ_fd)(9)

The current controller bandwidth is at least an order of magnitude higher than the outer speed controller. Hence the d-axis speed ω_m in the above equations can be considered to be a constant and ignored in the small signal analysis. Thus, the above equation can be rewritten in transfer function form as:

i_sd(s)v_sd(s) = G_c(s) = 1R_s + sL_s(10)

The small signal transfer function for q-axis current and q-axis voltage is the same as the above equation. The overall current loop transfer function is show below.

Induction motor vector control current loop PI controller

This transfer function is similar to the one obtained in the experiment Vector control of Induction motor. The PI controller proportional gain k_p and integral gain k_i can be obtained from the desired system cross-over frequency ω_i,c and phase margin Φ_i as given by Eqns. 11 through 13, which were derived in the earlier experiment.

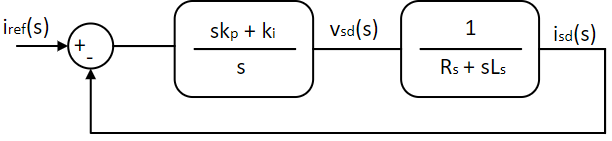
⇒ k_i,p = k_i,iω_i,c × tan(Φ_i - π2 + tan^-1(ω_i,cL_sR_s)) = C1 × k_i,i(11)

where,

C1 = 1ω_i,c × tan(Φ_i - π2 + tan^-1(ω_i,cL_sR_s))(12)

and

⇒ k²_i,i= ω²_i,c × (ω_i,cL_s)² + R²_a(ω_i,c × C1)² + 1(13)

Speed controller design

The mechanical system transfer function can be obtained from Eqn. 6. Ignoring the load torque as disturbance,

ω_mech(s)T_em(s) = G_s(s) = 1sJ + B(14)

Subtituing Eqn. 5 in Eqn. 14:

ω_mech(s)i_sq(s) = k_tG_s(s) = k_tsJ + B(15)

The inner current loop can be modelled as unity gain transfer function. This assumption is valid as long as the response time of inner current loop is magnitude higher than the outer speed loop. Or in other words, the cross-over frequency of inner current loop ω_i,c >> cross-over frequency of outer speed loop ω_s,c. Similar to current controller, the above system can be represented as shown below:

K_s(jω) = PI_s(jω) × G_s(jω) = k_s,ps + k_s,is × k_tJs + B(16)

The above system is similar to that of the current controller designed earlier and going through the same procedure, the speed controller's gains are obtained to be:

k_s,p = C2 × k_s,i(17)

where,

C2 = 1ω_s,c × tan(Φ_s - π2 + tan^-1(ω_s,cJB))(18)

and

k²_s,i= (ω_s,ck_t)² × (ω_s,cJ)² + B²(ω_s,c × C2)² + 1(19)

where, k_s,p and k_s,i are the speed Pi controller's proportional and integral gain.

Simulation of PMAC motor speed control

The above speed control model is simulated using Workbench in this section. The motor is assumed to be operating under steady-state condition and a step change is load torque is introduced at time t = 0.1 s. The resultant dynamic response is observed. Unlike previous experiments, where the motor was simulated from zero steady-state condition, here the motor is simulated starting from a non-zero steady-state condition. This rapidly accelerates the simulation due to possibility of using a larger step time due to smaller magnitude of load torque, reference speed or current change compared to starting from zero steady-state condition.

Motor model design

Open loop motor model

Create a new project, and add a new model and script file to the project.
Set this model file as the Start model/Function in project properties.

Open the script file and initialize all the model parameter as shown below from the parameters estimated in previous experiment.

Code

Public Module PM

    Public Rs As Native Double = 0.7 / 2 ! Stator Resistance

    Public Ls As Native Double = 0.5E-3 / 2 ! Stator leakage inductance

    Public P As Native Double = 8 ! Number of Poles

    Public J As Native Double = 50E-6 ! Rotor Inertia

    Private ke As Native Double = 0.0416 / (2 * π) ! Back emf constant

    Public λf As Native Double = ke / (√2 / √3)

    

    ! Steady state operating condition

    Public f As Native Double = 60 ! Operating frequency

    Public ωmech0 As Native Double = f * 4 * π / P ! Rotor speed in rad/sec

    Private ωsync As Native Double = ωmech0 * P / 2 ! Electrical speed/ rotating flux speed

    Private Tem As Native Double = 0.1 ! Electromagnetic torque

    Public Tl0 As Native Double = Tem ! Load torque

    Public Isd0 As Native Double = 0 ! d axis current

    Public Isq0 As Native Double = Tem / ((P / 2) * λf) ! q axis current

    Public λsd0 As Native Double = Ls * Isd0 + λf ! d axis flux

    Public λsq0 As Native Double = Ls * Isq0 ! q axis flux

    Public Vsd0 As Native Double = Rs * Isd0 - ωsync * Ls * Isq0 ! d axis stator voltage

    Public Vsq0 As Native Double = Rs * Isq0 + ωsync * (Ls * Isd0 + λf) ! q axis stator voltage

    Public Vs0 As Native Double = (√2 / √3) * √(Vsd0² + Vsq0²) ! Peak stator phase voltage

    Public VPh0 As Native Double = Math:ATan2(Vsq0, Vsd0) * 180 / π !Initial stator voltage phase shift

    

    ! Speed PI Loop

    Private ωc As Native Double = 100 ! Cross over frequency

    Private φm As Native Double = 60 * π / 180 ! Phase margin

    Private ωcKpbyKi As Native Double = Math:Tan(φm)

    Private kt As Native Double = (P / 2) * λf ! torque constant

    Public ki As Native Double = ωc² * J / (kt * √(1 + (Math:Tan(φm))²)) ! Speed loop integrator gain

    Public kp As Native Double = ωcKpbyKi * ki / ωc ! Speed loop proportional gain

    

    ! Current PI Loop

    Private ωci As Native Double = ωc * 10 ! Cross over frequency, 10 times outer speed loop

    Private φmi As Native Double = φm ! Phase margin

    Private ωciKpibyKii As Native Double = Math:Tan(φmi - π / 2 + Math:Atan(ωci * Ls / Rs))

    Public kii As Native Double = ωci * √((Rs² + (ωci * Ls)²) / (ωciKpibyKii² + 1)) ! Current loop integrator gain

    Public kpi As Native Double = ωciKpibyKii * kii / ωci ! Current loop proportional gain

End Module

The first section of the script file sets the motor parameters as obtained from the nameplate. It can be obtained by parameter estimation, similar to what was done in TInv_AD_IMParameter. The steady-state currents and voltages for the motor operating under rated speed and load-torque is calculated in the following section as per Eqns. 1 through 7. In the next section, the outer speed controller's PI gains are calculated using Eqns. 13 through 15 for system cross-over frequency of 100 rads/s and phase margin of 60°. The final section computes the inner speed controller's PI gains using Eqns. 17 through 19 for a cross-over frequency 10 times that of outer speed loop and the same phase margin.

Open the model file and within its properties set the Step time to 5E-5.
Set the Run time to 0.3.
Drag and drop a subsystem tool from the Toolbox which is present in Signal Routing tool class.

Inside the subsystem, drag and drop the following tools from the Toolbox and connect them as shown to create abc to dq transformation.

#	Tool type	Tool class	Tool name
1	In-port	Signal Routing	I
2	In-port	Signal Routing	I1
3	Constant	Signal Sources	Constant
4	Adder Subtractor	Math Block	Add
5	Elementary Function	Math Block	ElemF
6	Elementary Function	Math Block	ElemF1
7	Multiplier Divider	Math Block	Mul
8	Multiplier Divider	Math Block	Mul1
9	Demux	Signal Routing	DeMux
10	Demux	Signal Routing	DeMux1
11	Adder Subtractor	Math Block	Add1
12	Adder Subtractor	Math Block	Add2
13	Gain	Math Block	Gain
14	Gain	Math Block	Gain1
15	Concatenate	Matrix Manipulation	Concat
16	Out-port	Signal Routing	O

ABC to DQ transformation

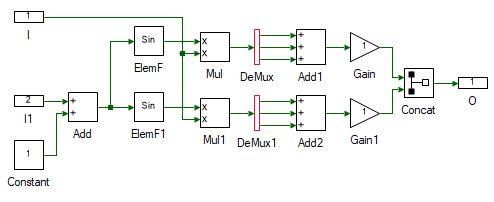
Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
I	Name	abc	Input abc signal.
I1	Name	theta	Input theta.
Constant	Magnitude	{0, 2 * π / 3, 4 * π / 3}	Muxed 3Φ phase shift signal.
Add	Arithmetic operation	+-	Add the cosine terms.
ElemF	Function	Cos
ElemF1	Function	Sin
DeMux	Number of Ports	3	Split the muxed signal to independent signal.
DeMux1	Number of Ports	3	Split the muxed signal to independent signal.
Add1	Number of ports	3	Add the cosine terms.
Add2	Number of ports	3	Add the sine terms.
Gain	Gain	√2 / √3	Scale by sqrt(2/3).
Gain1	Gain	-(√2) / √3	Scale by -sqrt(2/3).
Concat	Pivot Dimension	2	Combine the signal to form a column matrix.
O	Name	dq	Output dq.

Go back to the main motor model by clicking on the tab on the top.
Resize the subsystem so that all the ports can be seen. A tool can be resized by clicking and dragging any of the four squares in the tool's corner.

Drag and drop the following tools from the Toolbox to the model and connect them as shown to test if abc to dq is functioning as expected.

#	Tool type	Tool class	Tool name
1	Sine	Signal Sources	Sine
2	Constant	Signal Sources	Constant
3	Integrator	Math Block	Integrator
4	Mag-Time Scope	Display	Scope

ABC to DQ transformation

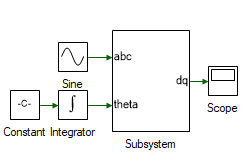
Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
Sine	Phase shift (in degrees)	{0, -120, -240}	Input abc signal.
Constant	Magnitude	2 * π * 1	Frequency of input signal in rads/s.
Integrator	Initial value	-π / 2	The d-axis is aligned with the rotor flux. In the later steps, the d-axis angle is obtained by integrating the d-axis speed which is computed. For now, it is connected to a constant.

Run the simulation and check if the results are dc value, with d-axis equal to zero and q-axis positive.

Create a new subsystem. Drag and drop the following tools from the Toolbox to the subsystem model and connect them as shown to create dq to abc transformation.

#	Tool type	Tool class	Tool name
1	In-port	Signal Routing	I
2	In-port	Signal Routing	I1
3	Constant	Signal Sources	Constant
4	Demux	Signal Routing	DeMux
5	Adder Subtractor	Math Block	Add
6	Elementary Function	Math Block	ElemF
7	Elementary Function	Math Block	ElemF1
8	Multiplier Divider	Math Block	Mul
9	Multiplier Divider	Math Block	Mul1
10	Adder Subtractor	Math Block	Add1
11	Gain	Math Block	Gain
12	Out-port	Signal Routing	O

ABC to DQ transformation

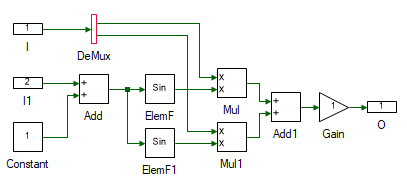
Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
I	Name	dq	Input dq signal.
I1	Name	theta	Input theta.
Constant	Magnitude	{0, 2 * π / 3, 4 * π / 3}	Muxed 3Φ phase shift signal.
Add1	Arithmetic operation	+-	Add the cosine terms.
ElemF	Function	Cos
ElemF1	Function	Sin
Add1	Arithmetic operation	+-	Subtract the cosine and sine terms.
Gain	Gain	√2 / √3	Scale by sqrt(2/3).
O	Name	abc	Output abc.

Go back to the main motor model by clicking on the tab on the top.
Resize the subsystem so that all the ports can be seen. A tool can be resized by clicking and dragging any of the four squares in the tool's corner.

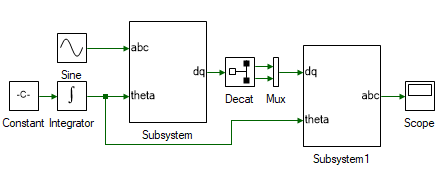
Drag and drop the following tools from the Toolbox to the model and connect them as shown to test if abc to dq is functioning as expected. The output of ABCtoDQ is a column matrix and input of DQtoABC is muxed signal. Hence these must be converted.

#	Tool type	Tool class	Tool name
1	Decatenate	Matrix Manipulation	Decat
2	Mux	Signal Routing	Mux

DQ to ABC transformation

Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
Decat	Pivot Dimension	2	Split along the row

Run the simulation and check if the results are same as the input.
Delete the Decat and Mux tool.

Next step is to determine the stator flux of the motor as given in Eqn. 13. Create another subsystem and drag and drop the tools shown and connect them as shown to implement the above equation.

#	Tool type	Tool class	Tool name
1	In-port	Signal Routing	I
2	In-port	Signal Routing	I1
3	In-port	Signal Routing	I2
4	Constant	Signal Sources	Constant
5	Multiplier Divider	Math Block	Mul
6	Multiplier Divider	Math Block	Mul1
7	Gain	Math Block	Gain
8	Adder Subtractor	Math Block	Add
9	Integrator	Math Block	Integrator
10	Out-port	Signal Routing	O

PMAC motor stator flux

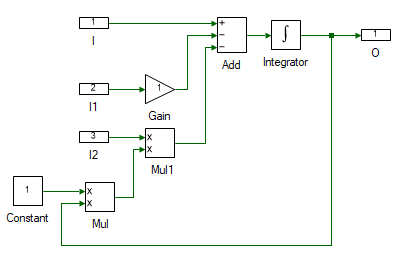
Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
I	Name	vsdq	Stator voltage dq signal, v_sdq.
I1	Name	isdq	Stator current dq signal, i_sdq.
I2	Name	wd	d-axis speed, ω_d.
Gain	Gain	PM:Rs	Stator resistance, R_r.
Constant	Magnitude	[[0, -1], [1, 0]]	Rotational matrix
Add	Number of ports	3
Add	Add	Arithmetic operation	+--
Integrator	Initial value	[[PM:λsd0], [PM:λsq0]]	Initial stator flux linkage.
O	Name	fsdq	Stator dq flux, λ_sdq.

Next step is to determine the stator currents from the flux. as given in Eqns. 3 and 4. Drag and drop the tools shown and connect them as shown to implement the above equation.

#	Tool type	Tool class	Tool name
1	Constant	Signal Sources	Constant1
2	Adder Subtractor	Math Block	Add
3	Gain	Math Block	Gain
4	Decatenation	Matrix Manipulation	Decat

Induction motor dq currents

Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
Constant1	Magnitude	[[PM:λf],[0]]	λ_rq = 0.
Add	Arithmetic operation	+-	Difference between stator and rotor flux. Eqns. 3 and 4.
Gain	Gain	1/PM:Ls	Flux divided by stator inductance to obtain the stator dq currents.
Decat	Pivot Dimension	2	Split into i_sd and i_sq.

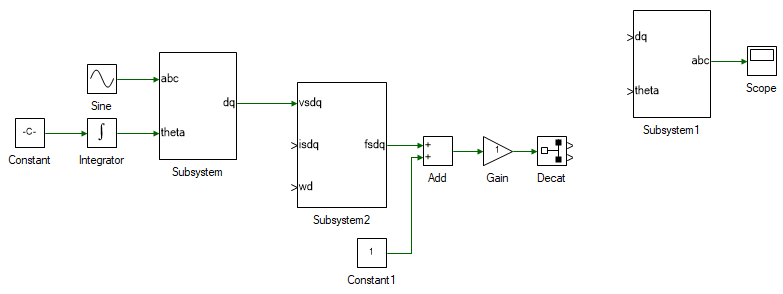
All of the model designed so far is transferred into a subsystem. Select all the tools and connection (CtrlA), and copy it (CtrlC). Delete the selection. Add a new subsystem to the blank model and within the subsystem paste the copied object (CtrlV). This newly created subsystem represents the PMAC motor model.

Next step is to determine the motor speed to close the loop. This is computed using Eqns. 5 through 7. Add the following tools and connect them as shown.

#	Tool type	Tool class	Tool name
1	Mux	Signal Routing	Mux
2	Gain	Math Block	Gain1
3	Step	Signal Sources	Step
4	Adder Subtractor	Math Block	Add1
5	Gain	Math Block	Gain2
6	Integrator	Math Block	Integrator
7	Scope	Display	Scope1

PMAC motor electromagnetic torque and speed

Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
Gain1	Gain	(PM:P / 2) * PM:λf	Eqn. 5. T_em calculation.
Step	Initial value	PM:Tl0	Initial steady-state load torque.
	Step	Final value	PM:Tl0 / 2	Step change in load torque.
	Step	Step time	0.1	Change load torque at time t = 0.1 s.
Add1	Arithmetic operation	+-	Eqn. 6. T_em - Tl.
Gain2	Gain	1 / PM:J	Eqn. 6.
Integrator1	Initial value	PM:ωmech0	Eqn. 6, rotor mechanical speed calculation.

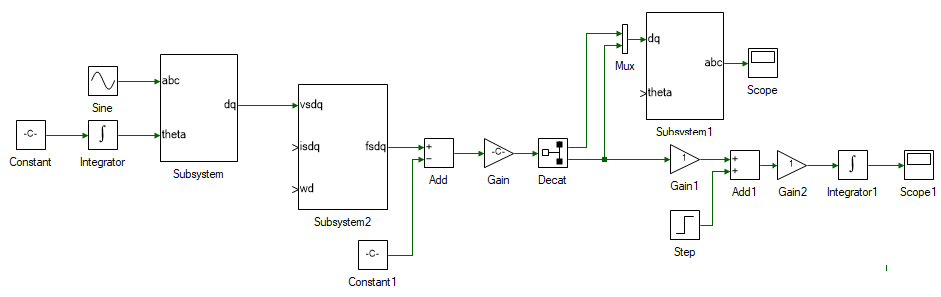
All that remains is to close the loop. Delete the Constant tool connected to the abc → dq subsystem. This was initially used as the d-axis speed and is no longer needed since we have the actual d-axis speed, aligned with rotor flux. Replace the Constant tool on the left-most corner and replace it with a Gain tool and set the Gain to PM:P / 2. This converts the rotor mechanical speed to d-axis speed as given by Eqn. 7. Connect the output of Integrator1 which is ω_mech to input of the newly added gain block. Output of the gain block is ω_d. Connect this to the motor flux subsystem. Output of Integrator connected to the newly added gain is θ_da, which must be connected to dq → abc subsytem's theta input. The stator dq currents for the stator flux subsystem, i_sdq is obtained by connecting the output of Gain block, which is also the input of the Decat block. The overall induction motor dq model, with d-axis aligned with rotor flux, is shown below.

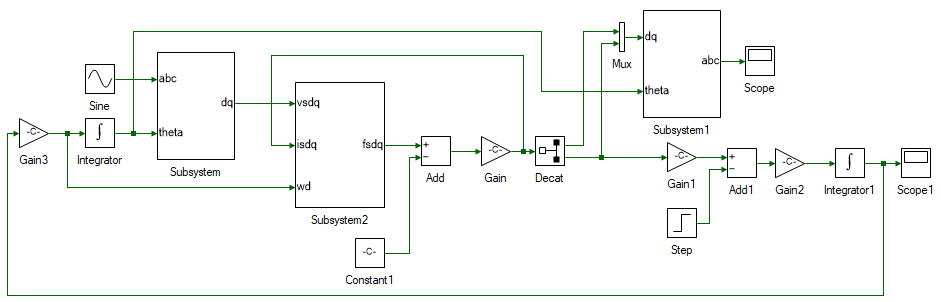
Set the stator 3φ voltage in the Sine block.

Tool name	Property field	Property value	Comments
Sine	Magnitude	PM:Vs0	Steady-state peak stator phase voltage magnitude
	Sine	Phase shift (degrees)	{PM:Vph0, PM:Vph0 - 120, PM:Vph0 - 240}	Stead-state stator voltage phase shift
	Sine	Frequency (Hz)	PM:f	Stead-state stator voltage frequency

Add scope to observe, abc and dq stator voltages and currents, motor speed, electromagnetic torque and any other values you might be interested in looking at.
Run the simulation and observe the results.
This is the response of the motor to a step change in load torque. The speed settles back to synchronous speed even under open loop condition. If the load was increased rather than being reduced as in this case, the motor would become unstable Change to Final value in the Step block to PM:Tl0 * 1.1, i.e., the load is increased by 10%. Rerun the simulation and observe the results. The rotor quickly decelerates due to demanding more than the generatable peak electromagnetic torque for the applied voltage. This is overcome by dynamically adjusting the applied voltage based on load-torque demand by using PI controller as seen in the following section.

If any runtime exception occurs, use the DataPeek window, docked on the right, to look at each of the tool's input, output and parameter right before the exception occurred. This tool can be used to observe the value of any tool or code variables at any time. Click on the Data peek show selected icon in the DataPeek window and select any tool to look at its value. Similarly, to look at the value of a variable in Script file, place the cursor on the variable and select it by double clicking. Its value will pop-up in the DataPeek window.

Motor current control

In this section, the current through the motor is controlled using a PI controller.

Within the motor model subsystem, remove the Sine tool and replace it with an Inport and name it Vabc. Similarly remove the Step tool and replace it with an Inport and name it Tl. These are the two inputs to the motor model. The outputs of the motor model are stator currents and rotor mechanical speed. To get the out of the subsystem, replace the Scope tool with Outport tool and name it Iabc. Similarly replace the Scope1 tool with Outport tool and name it ωmech.
In the main model file add a subsystem, where the d-axis PI current controller will be modelled. Double click and open the subsystem.

Drag and drop the following tools from the Toolbox to the subsystem model and connect them as shown.

#	Tool type	Tool class	Tool name
1	In-port	Signal Routing	I
2	In-port	Signal Routing	I1
3	Adder Subtractor	Math Block	Add
4	Gain	Math Block	Gain
5	Gain	Math Block	Gain1
6	Integrator	Math Block	Integrator
7	Adder Subtractor	Math Block	Add2
8	Saturation	Non-linear	Saturation
9	Out-port	Signal Routing	O

PI current controller

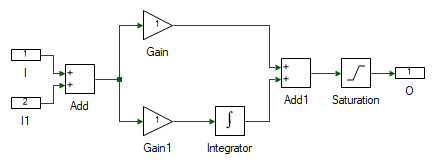
Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
I	Name	Ref	Desired reference motor current.
I1	Name	Fbk	Actual motor current.
Add	Arithmetic operation	+-	Difference between the desired and actual motor current.
Gain	Gain	PM:kpi	Current controller proportional gain.
Gain1	Gain	PM:kii	Current controller integral gain.
Integrator	Integrator Type	Anti-windup	Reason explained later.
	Integrator	Initial value	PM:Vsd0	Steady-state stator d-axis voltage.
	Integrator	Upper Limit	20
	Integrator	Lower Limit	-20
Saturation	Upper Limit	20
Saturation	Saturation	Lower Limit	-20
O	Name	Out	Applied terminal voltage to generate the desired current profile.

When there is a large difference between the desired current and the actual current, the PI controller produces a large output voltage to quickly correct this error. In real-world, the magnitude of this voltage is limited either due to available DC bus voltage or due to motor and power electronics voltage ratings. Hence in practical implementation of PI controller, the output of the PI controller is saturated to the maximum possible voltage. So, during transient conditions, when the actual current is different from the desired current, the Integrator in the PI controller rapidly builds up its output to a large value due to persistent input error. When the error does goes back to zero, this large output built up by the integrator does not die down and cause the actual current to overshoot the desired the value, causing the error to go negative, which causes the integrator output to fall, but it will end up falling by much larger value than desired causing the current to undershoot. This keeps repeating, and this oscillation will die down slowly. To avoid this, the value up to which integrator is active is clamped by setting it to Anti-windup. If the integrator output reaches this value, the integrator is disabled until the polarity of the error reverses. This improves the response of the system significantly.

Create a copy of the PI subsystem for q-axis current control.
Within the copied subsystem set the Integrator's Initial value to PM:Vsq0.
The output of the PI controller are dq voltages. These needs to converted to abc voltages before inputting them to the motor model. To do this, copy and paste the dq-abc subsystem previously implemented within the motor model.
The output of the motor model is stator currents in abc domain. To connect them back to the PI current controller's feedback they need to be transformed to dq currents. To do this, copy and paste the abc-abc subsystem previously implemented within the motor model.

The overall current controller system is shown below, after addition of few more tools listed in the following steps:

PMAC motor current control.

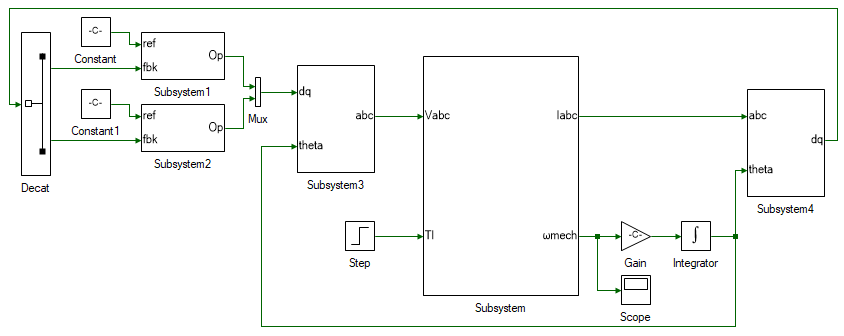
The motor model is within Subsystem. The d and q axis PI current controllers are within Subsystem1 and Subsystem2 respectively. The dq stator voltage output of the PI controllers are converted to abc voltages using dq-abc transformation within Subsystem3. Finally, the stator abc motor currents are converted to dq currents using abc-dq transformation within Subsystem4.

Add the following tools and connect them as shown in the figure above:

#	Tool type	Tool class	Tool name
1	Decat	Matrix manipulation	Decat
2	Constant	Signal Sources	Constant
3	Constant	Signal Sources	Constant1
4	Mux	Signal Routing	Mux
5	Step	Signal Sources	Step
6	Gain	Math Block	Gain
7	Integrator	Math Block	Integrator
8	Scope	Display	Scope

Change the properties of each tool to values listed in table below.

Tool name	Property field	Property value	Comments
Decat	Pivot dimension	2	Split into i_sd and i_sq.
Constant	Magnitude	PM:isd0	Stator d-axis current, ideally set to 0 unless field-weaking is used to increase the speed limit.
Constant1	Magnitude	PM:isd0	Stator q-axis current.
Step	Initial value	PM:Tl0	Initial steady-state load torque.
	Step	Final value	PM:Tl0 / 2	Step change in load torque.
	Step	Step time	0.1	Change load torque at time t = 0.1 s.
Gain	Gain	PM:P / 2	Eqn. 7.
Integrator	Initial value	-π / 2	The d-axis is aligned with the rotor flux. In the later steps, the d-axis angle is obtained by integrating the d-axis speed which is computed.

Run the simulation and observe the rotor speed. The rotor speed is maintained a constant only as long as the load torque does not change. Once the load torque decrease, the rotor accelerates because the electromagnetic torque being produced is higher than the load torque. In reality, this will not be the case and the speed will settle down either due to friction or due to limited DC bus voltage.

The current controller is applicable in systems where the torque is to be directly controlled. In application where to rotor speed is to be controlled, the q-axis current PI controller is further extended by addition of an outer speed PI controller.

Motor speed control

In this section, the speed of the motor is controlled using a PI controller.

Replace the Constant1 block for q-axis current reference with a PI controller subsystem, output of which will be the reference q-axis current.

Change the properties of the tools within the newly pasted PI controller to the values listed the table:

Tool name	Property field	Property value	Comments
Gain	Gain	PM:kp	Speed controller proportional gain.
Gain1	Gain	PM:ki	Speed controller integral gain.
Integrator	Initial value	PM:Isq0	Steady-state stator q-axis current.
Integrator	Upper Limit	5	Maximum stator current.
Integrator	Lower Limit	-5	Minimum stator current.
Saturation	Upper Limit	5	Maximum stator current.
Saturation	Saturation	Lower Limit	-5	Minimum stator current.

Connect the feedback input to motor speed from the motor model subsystem. Apply a constant speed for reference, and set the Magnitude to PM:ωmech0. The overall system is shown below:
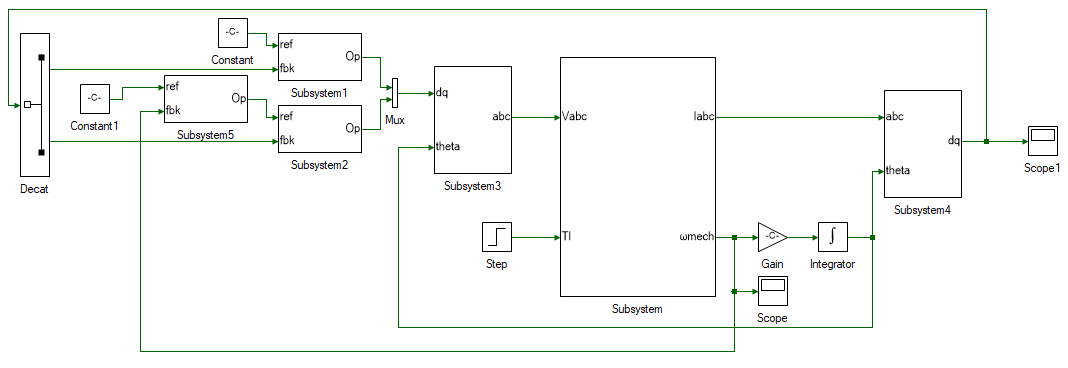
Run the simulation and observer if motor steady state speed matches the reference speed.

This concludes the simulation of PMAC motor vector control. In the following section, a pre-built PMAC motor vector control model is run in real-time.

Real-time vector control of Induction motor

Assemble the PMAC motor-DC motor set as shown below:
1. DC Generator (one with A-quad-B encoder mounted on its back).
2. PMAC Motor.
3. Oldham coupler. Tighten if loose using M2.5 hex wrench.
4. Oldham coupling disk. Attach it to the motor and generator coupling.
5. Safety enclosure. The coupling unit resides inside the safety enclosure.
6. M4 hex socket-head screws - x8.
7. M2.5 hex wrench - Tighten the motor and generator onto the safety enclosure.
8. 2048-line A-quad-B encoder - Attach the encoder cable to the A-quad-B encoder.
Connect the PMAC motor terminals to the Inverter 1 terminals such that the color of both these terminals matches one another. Connect the DC generator -ve (black terminal) to Inverter 2 A phase (black terminal) and DC generator +ve (red terminal) to Inverter 2 B phase (red terminal).

Warning

Ensure that the DC power supply is turned off before making the connections. If the DC power supply does not have a dedictated ground terminal, that connection can be left floating. If present, it is strongly recommended that it be connected to the three-inverter module's ground terminal to mitigate any electrical hazard.
Open Workbench and pin the Explorer and Properties dock.
Navigate to and open the PMVectorControl project file in Experiment7\Realtime folder usually in the following location: C:\Program Files (x86)\Sciamble\WorkBench v1\Examples\CUSPLab\AdvancedDrives.
Expand the project and open the RotorInit model file shown below:

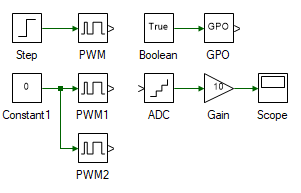
The incremental encoder used does not output the actual absolute position of the rotor. Rather it outputs a pulse when the rotor turns by a certain angle. Since the initial rotor position cannot be known using the incremental encoder, it is forcefully initialized to a pre-determined position. This is achieved by briefly connecting the phase-A winding to V_dc and the phase-B and C winding to 0, as done so in RotorInit model file. This ensures that the initial rotor magnetic flux axis is aligned along the stator phase-A winding axis.
Open project properties and set the Start model/Function to RotorInit.
Turn ON the DC power supply and set the voltage to 40 V.
Ensure that button on the top dock, to transition to real-time mode, is pressed. Click the button.
After about 5s, click the button to stop the model.
Open the ModelFile model file shown below:

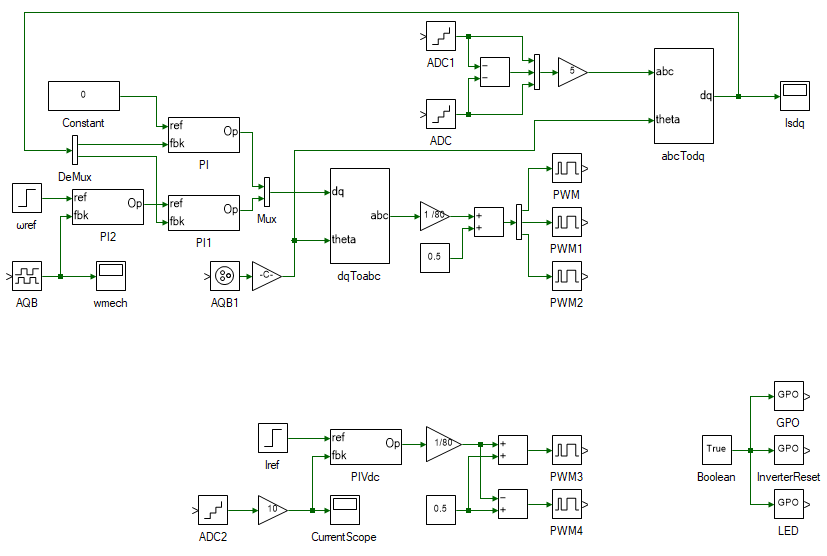
The top section of the model consists of the PMAC motor vector control and is merely a replication of the simulation model developed earlier with few additions to enable real-time control. On the left is the speed PI controller, followed by the d and q axis current PI controller, the output of which is the dq terminal voltages. The dq voltages are converted to abc voltages in the following subsystem. In the simulation model, this terminal voltage signal was connected to the motor model. In this case it is converted to inverter's PWM duty cycles and routed through the PWM toolbox, to control the induction motor in real-time. The output of the Induction motor model is the stator and rotor currents, and the rotor speed. In real-time mode, the stator currents are measured from the actual motor currents by means of ADCs and the speed is measured from the actual motor's A-quad-B encoder. Similar to the PWM signal, the stator currents are routed through the ADC blocks and the rotor speed is routed through AQB block. This allows the same model to be run in both simulation and in real-time. During simulation, the tools from the Hardware Integration merely act as a 1:1 buffer and bypasses all input signals. In real-time, these tools read data from or write data to the real-time controller's peripherals.

The bottom section consists of the DC motor current control. This is used to emulate the load torque.
Turn ON the DC power supply and set the voltage to 40 V.
Ensure that button on the top dock, to transition to real-time mode, is pressed. Click the run button.
Observe the speed and current result in the scope. Click the to focus the result. After about 5 s, stop data logging by clicking .
Turn OFF the DC power supply.
If necessary, repeat the experiment for different loop cross-over frequencies and phase margins.
Turn OFF the DC power supply and disconnect all the connections including the USB.

Lab report and reading assignment

List the k_p and k_i values of the current and speed PI controller.
Attach the plot of dq stator currents and rotor speed from simulation for without controller, with current controller and with speed controller for both increasing and decreasing step load torque.
In current controller mode simulated, if the coefficient of friction B in Eqn. 6 was given to be 200E-6, at what speed would the rotor have settled to when the load torque was halved.
Design a PI controller to control the position of the rotor.

Reference

"Analysis and Control of Electric Drives: Simulations and Laboratory Implementation," Ned Mohan and Siddharth Raju, Wiley Publication.