Vector control of Induction motor

• August 03, 2019
• 3 hours to complete
• Workbench v1.5
• • 
  • 

Introduction

In this experiment, a mathematical model of an induction motor will be simulated based on the parameters estimated in the previous experiment. For this, unlike the previous experiment where the model was in abc domain, the motor will be modeled in dq frame. With proper alignment of the dq frame, the motor model becomes simpler compared to motor modelled in abc frame. The major advantage of this approach, other than the reduction in simulation run-time, is the ease of PI controller design to control motor speed, current or position. In addition to simulation, the controller designed will also be evaluated on an actual induction motor in real-time.

Theoretical background

Motor model

The following set of equations represents a linearized induction motor in the dq frame [1]:

v_sd = R_si_sd - ω_dλ_sq + dλ_sddt(1)

v_sq = R_si_sq + ω_dλ_sd + dλ_sqdt(2)

v_rd = R_ri_rd - ω_dAλ_rq + dλ_rddt(3)

v_rq = R_ri_rq + ω_dAλ_rd + dλ_rqdt(4)

T_em = P2(λ_rqi_rd - λ_rdi_rq)(5)

λ_sd = L_si_sd + L_mi_rd(6)

λ_sq = L_si_sq + L_mi_rq(7)

λ_rd = L_mi_sd + L_ri_rd(8)

λ_rq = L_mi_sq + L_ri_rq(9)

T_em = T_l + Jdω_mechdt + Bω_mech(10)

ω_d = P2ω_mech + ω_dA(11)

where

1. V_sd, V_sq, V_rd and V_rq : stator d, stator q, rotor d, and rotor q axis voltage respectively

2. I_sd, I_sq, I_rd and I_rq : stator d, stator q, rotor d, and rotor q axis current respectively

3. λ_sd, λ_sq, λ_rd and λ_rq : stator d, stator q, rotor d, and rotor q axis flux-linkage respectively

4. R_s : stator resistance

5. R_r : reflected rotor resistance

6. L_m : Per-phase mutual inductance

7. L_s : L_ls + L_m where, L_ls is the stator leakage inductance

8. L_r : L_lr + L_m where, L_lr is the rotor leakage inductance

9. J : rotor inertia

10. B : coefficient of viscous friction

11. P : Number of stator poles

12. T_em : output/electromagnetic torque

13. T_l : load torque

14. ω_mech : rotor mechanical speed

15. ω_d : d-axis rotation speed with respect to stator A-phase magnetic axis

16. ω_da : d-axis rotation speed with respect to rotor A-phase magnetic axis

The dq quantities are obtained from their corresponding abc by the following equations:

dq = √(2/3) × (a × e^-jθ + b × e^{-jθ + 2π/3} + c × e^{-jθ + 4π/3})(12)

where, θ is obtained by integrating the d-axis speed with respect to corresponding magnetic axis.

In case of induction motor vector control, the d-axis is aligned along the rotor flux axis, which implies, λ_rq = 0. For the motor under consideration, squirrel cage induction motor where the rotor bars are shorted, the rotor voltage v_sd and v_sq are both zero. Substituting these and combining the d and q equation, leads to the following simplified equations:

v_sdq = R_si_sdq - ω_dλ_sqd + dλ_sdqdt

⇒ dλ_sdqdt = v_sdq - R_si_sdq + ω_dλ_sqd(13)

From Eqns. 3 and 8

0 = R_ri_rd + dλ_rddt = R_rλ_rd - L_mi_sdL_r + dλ_rddt

⇒ dλ_rddt = L_mτ_ri_sd - λ_rdτ_r(14)

where, τ_r = L_rR_r

From Eqns. 4 and 9

0 = R_ri_rq + ω_dAλ_rd

⇒ ω_dA = -R_ri_rqλ_rd = L_mτ_rλ_rdi_sq(15)

From Eqns. 5 and 9

T_em = -P2λ_rdi_rq = P2L_mL_rλ_rdi_sq(16)

Equations 6 through 16, represent the simplified motor model, under the condition that the d-axis is aligned with rotor flux-axis.

Current controller design

In current control mode, the stator d and q axis currents are controlled under varying load conditions. Under steady state condition, the rotor flux is solely a function of i_sd as can be inferred from Eqn. 3 and 8. Throughout the motor operation, the i_sd is maintained a constant at rated value to have fast dynamic response, i.e., produce maximum torque with minimum i_sq. This value is calculated as follows.

Under steady state condition, the derivative terms in Eqns. 1 through 4 become zero, ω_d = ω_sync = 2πf and ω_dA = s * ω_sync = ω_slip where s is the slip and f is the frequency of the applied voltage. Assume that the d-axis is aligned with stator voltage space vector at time t = 0 then, v_sq = 0 and v_sd = √(3/2) x V_a where, V_a is the rated peak phase voltage. This obviously will not be the case in steady state, because the d-axis is aligned with rotor flux axis which is not in phase with applied stator voltage. But this shall be compensated for, later in the computation. Substituting these into Eqn. 1 through 4 yields:

R_si_sd - ω_sync(L_si_sq + L_mi_rq)= √(3/2) × V_a(17)

R_si_sq + ω_sync(L_si_sd + L_mi_rd) = 0(18)

R_ri_rd - s × ω_sync(L_mi_sq + L_ri_rq) = 0(19)

R_ri_rq + s × ω_sync(L_mi_sd + L_ri_rd) = 0(20)

From the above four equations, the stator and rotor dq currents can be computed, using which the rotor dq flux linkage can be computed by using Eqn. 8 and 9. In vector control, where d-axis is aligned with rotor flux axis, the λ_rq must be equal to zero. This will not be case here, since we aligned the d-axis to stator voltage. To compensate for this, all the computed dq values are rotated by:

θ_r = -tan^-1λ_rqλ_rd(21)

which will make λ_rq = 0 as well as give the rated i_sd for d-axis aligned with rotor flux.

Having determined the reference d axis stator current, lets proceed with designing the controller for the current loop. From Eqn. 6, 7 and 8, it can be easily derived that:

λ_sd = σL_si_sd+ L_mL_rλ_rd(22)

λ_sq = σL_si_sq(23)

where, σ is the leakage factor of the induction motor given by, σ = 1 - L²_mL_sL_r

Substituting these into Eqn. 1 and 2 yields:

v_sd = R_si_sd + σL_sdi_sddt + L_mL_rdλ_rddt - ω_dσL_si_sq(24)

v_sq = R_si_sq + σL_sdi_sqdt + ω_dL_mL_rλ_rd - ω_dσL_si_sd(25)

For controller design, the last two terms can be ignored as disturbances. The resulting equation in transfer function form is given below:

i_sd(s)v_sd(s) = G_c(s) = 1R_s + sσL_s(26)

The transfer function for the q-axis current ends up being the same as d-axis current. Hence tuning the PI loop for one of the axis would suffice. The overall system is shown below:

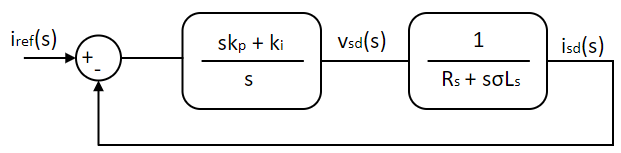
The k_i,p and k_i,i gain values are adjusted to have the desired transient response. There are multiple ways to quantify the desired response. In time domain, usually the desired rise time and overshoot for a step input is mentioned and the gains are adjusted to satisfy this requirement. Alternatively, in frequency domain, the desired phase margin and cross-over frequency are mentioned. We shall go the latter route since it gives a better picture of the system stability. The steady state response of the system is obtained by substituting s = jω in Eqn. 9.

K_c(jω) = PI_c(jω) × G_c(jω) = jωk_i,p + k_i,ijω × 1jωσL_s + R_s(27)

The above system is tuned for desired phase margin of Φ_i at cross-over frequency ω_i,c as follows. At the cross-over frequency, the system gain equals 1 and the system phase shift equals -π + Φ_i. Substituting this into Eqn. 10:

∠K_c(jω_i,c) = -π + Φ_i = -π2 + tan^-1(ω_i,ck_i,pk_i,i) - tan^-1(ω_i,cL_sR_s)

⇒ ω_i,ck_i,pk_i,i = tan(Φ_i - π2 + tan^-1(ω_i,cL_sR_s))

⇒ k_i,p = k_i,iω_i,c × tan(Φ_i - π2 + tan^-1(ω_i,cσL_sR_s)) = C1 × k_i,i(28)

where,

C1 = 1ω_i,c × tan(Φ_i - π2 + tan^-1(ω_i,cσL_sR_s))(29)

and

|K_c(jω_i,c)| = 1 = |jω_i,ck_i,p + k_i,ijω_i,c × 1jω_i,cL_s + R_s|

⇒ (ω_i,ck_i,p)² + k²_i,i = ω²_i,c((ω_i,cL_s)² + R²_a)

⇒ k²_i,i= ω²_i,c × (ω_i,cL_s)² + R²_a(ω_i,c × C1)² + 1(30)

Given the desired Φ_i and ω_i,c, and the motor parameters, the PI gains can be solved using Eqns. 28 through 30.

Speed controller design

The mechanical system transfer function can be obtained from Eqn. 10. Ignoring the load torque as disturbance,

ω_mech(s)T_em(s) = G_s(s) = 1sJ + B(31)

Using Eqn. 8, Eqn. 16 can be alternatively represented as given below, under vector control in steady state:

T_em = P2L²_mL_ri_sd,refi_sq = k_t × i_sq(32)

The inner current loop can be modelled as unity gain transfer function. This assumption is valid as long as the response time of inner current loop is magnitude higher than the outer speed loop. Or in other words, the cross-over frequency of inner current loop ω_i,c >> cross-over frequency of outer speed loop ω_s,c. Similar to current controller, the above system can be represented as shown below:

K_s(jω) = PI_s(jω) × G_s(jω) = k_s,ps + k_s,is × k_tJs + B(33)

The above system is similar to that of the current controller designed earlier and going through the same procedure, the speed controller's gains are obtained to be:

k_s,p = C2 × k_s,i(34)

where,

C2 = 1ω_s,c × tan(Φ_s - π2 + tan^-1(ω_s,cJB))(34)

and

k²_s,i= (ω_s,ck_t)² × (ω_s,cJ)² + B²(ω_s,c × C2)² + 1(35)

where, k_s,p and k_s,i are the speed Pi controller's proportional and integral gain.

Simulation of Induction motor speed control

The above speed control model is simulated using Workbench in this section.

Open loop motor model

1. Create a new project, and add a new model and script file to the project.

2. Set this model file as the Start model/Function in project properties.

3. Open the script file and initialize all the model parameter as shown below from the parameters estimated in previous experiment.

   Code

   Public Module IM
   
       Public f As Native Double = 50 ! Rated frequency
   
       Public Rs As Native Double = 1.79 ! Stator Resistance
   
       Public Rr As Native Double = 1.05 ! Rotor Resistance
   
       Public Lls As Native Double = 5E-3 ! Stator leakage Inductance
   
       Public Llr As Native Double = 5E-3 ! Rotor leakage Inductance
   
       Public Lm As Native Double = 30E-3 ! Mutual Inductance
   
       Public Ls As Native Double = Lm + Lls ! Stator Inductance
   
       Public Lr As Native Double = Lm + Llr ! Rotor Inductance
   
       Public J As Native Double = 150E-6 ! Rotor Inertia
   
       Public B As Native Double = 100E-6 ! Coefficient of Viscous friction
   
       Public P As Native Double = 4 ! Number of poles
   
       Public Vllrms As Native Double = 14.7 ! Rated line to line voltage
   
       Public slip As Native Double = 0.1 ! Rated slip
   
       Public ωsyn As Native Double = 2 * π * f ! Synchronous speed at rated frequency
   
       Public ωm As Native Double = (1 - slip) * ωsyn ! Speed at rated slip
   
       Public Va As Native Double = VLLrms * √2 / √3 ! Phase voltage peak
   
       Public τr As Native Double = Lr / Rr
   
   End Module
   
   

4. Open the model file and within its properties set the Step time to 5E-5.

5. Drag and drop a subsystem tool from the Toolbox which is present in Signal Routing tool class.

6. Subsystem is merely an enclosure within which more tools can be added. Double click the subsystem to open it.

7. Drag and drop the following tools from the Toolbox to the subsystem model and connect them as shown to create abc to dq transformation, given in Eqn. 12.

   #	Tool type	Tool class	Tool name
   1	In-port	Signal Routing	I
   2	In-port	Signal Routing	I1
   3	Constant	Signal Sources	Constant
   4	Adder Subtractor	Math Block	Add
   5	Elementary Function	Math Block	ElemF
   6	Elementary Function	Math Block	ElemF1
   7	Multiplier Divider	Math Block	Mul
   8	Multiplier Divider	Math Block	Mul1
   9	Demux	Signal Routing	DeMux
   10	Demux	Signal Routing	DeMux1
   11	Adder Subtractor	Math Block	Add1
   12	Adder Subtractor	Math Block	Add2
   13	Gain	Math Block	Gain
   14	Gain	Math Block	Gain1
   15	Concatenate	Matrix Manipulation	Concat
   16	Out-port	Signal Routing	O

   

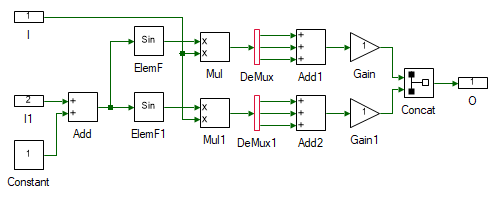
8. Change the properties of each tool to values listed in table below.

   Tool name	Property field	Property value	Comments
   I	Name	abc	Input abc signal.
   I1	Name	theta	Input theta.
   Constant	Magnitude	{0, 2 * π / 3, 4 * π / 3}	Muxed 3Φ phase shift signal.
   Add	Arithmetic operation	+-	Add the cosine terms.
   ElemF	Function	Cos
   ElemF1	Function	Sin
   DeMux	Number of Ports	3	Split the muxed signal to independent signal.
   DeMux1	Number of Ports	3	Split the muxed signal to independent signal.
   Add1	Number of ports	3	Add the cosine terms.
   Add2	Number of ports	3	Add the sine terms.
   Gain	Gain	√2 / √3	Scale by sqrt(2/3).
   Gain1	Gain	-(√2) / √3	Scale by -sqrt(2/3).
   Concat	Pivot Dimension	2	Combine the signal to form a column matrix.
   O	Name	dq	Output dq.

9. Go back to the main motor model by clicking on the tab on the top.

10. Resize the subsystem so that all the ports can be seen. A tool can be resized by clicking and dragging any of the four squares in the tool's corner.

11. Drag and drop the following tools from the Toolbox to the model and connect them as shown to test if abc to dq is functioning as expected.

    #	Tool type	Tool class	Tool name
    1	Sine	Signal Sources	Sine
    2	Constant	Signal Sources	Constant
    3	Integrator	Math Block	Integrator
    4	Mag-Time Scope	Display	Scope

    

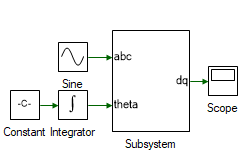
12. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    Sine	Phase shift (in degrees)	{0, -120, -240}	Input abc signal.
    Constant	Magnitude	2 * π * 1	Frequency of input signal in rads/s.

13. Run the simulation and check if the results are dc value, with d-axis equal to zero and q-axis negative.

14. Drag and drop the following tools from the Toolbox to the subsystem model and connect them as shown to create dq to abc transformation.

    #	Tool type	Tool class	Tool name
    1	In-port	Signal Routing	I
    2	In-port	Signal Routing	I1
    3	Constant	Signal Sources	Constant
    4	Demux	Signal Routing	DeMux
    5	Adder Subtractor	Math Block	Add
    6	Elementary Function	Math Block	ElemF
    7	Elementary Function	Math Block	ElemF1
    8	Multiplier Divider	Math Block	Mul
    9	Multiplier Divider	Math Block	Mul1
    10	Adder Subtractor	Math Block	Add1
    11	Gain	Math Block	Gain
    12	Out-port	Signal Routing	O

    

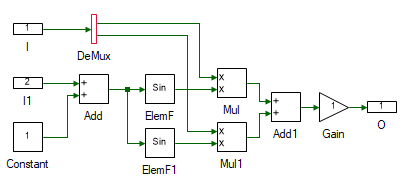
15. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    I	Name	dq	Input dq signal.
    I1	Name	theta	Input theta.
    Constant	Magnitude	{0, 2 * π / 3, 4 * π / 3}	Muxed 3Φ phase shift signal.
    Add1	Arithmetic operation	+-	Add the cosine terms.
    ElemF	Function	Cos
    ElemF1	Function	Sin
    Add1	Arithmetic operation	+-	Subtract the cosine and sine terms.
    Gain	Gain	√2 / √3	Scale by sqrt(2/3).
    O	Name	abc	Output abc.

16. Go back to the main motor model by clicking on the tab on the top.

17. Resize the subsystem so that all the ports can be seen. A tool can be resized by clicking and dragging any of the four squares in the tool's corner.

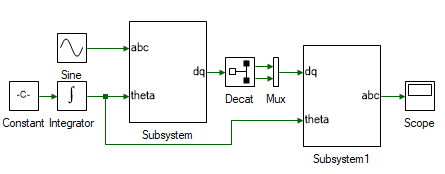
18. Drag and drop the following tools from the Toolbox to the model and connect them as shown to test if abc to dq is functioning as expected. The output of ABCtoDQ is a column matrix and input of DQtoABC is muxed signal. Hence these must be converted.

    #	Tool type	Tool class	Tool name
    1	Decatenate	Matrix Manipulation	Decat
    2	Mux	Signal Routing	Mux

    

19. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    Decat	Pivot Dimension	2	Split along the row

20. Run the simulation and check if the results are same as the input.

21. Delete the Decat and Mux tool.

22. Next step is to determine the stator flux of the motor as given in Eqn. 13. Create another subsystem and drag and drop the tools shown and connect them as shown to implement the above equation.

    #	Tool type	Tool class	Tool name
    1	In-port	Signal Routing	I
    2	In-port	Signal Routing	I1
    3	In-port	Signal Routing	I1
    4	Constant	Signal Sources	Constant
    5	Multiplier Divider	Math Block	Mul
    6	Multiplier Divider	Math Block	Mul1
    7	Gain	Math Block	Gain
    8	Adder Subtractor	Math Block	Add
    9	Integrator	Math Block	Integrator
    10	Out-port	Signal Routing	O

    

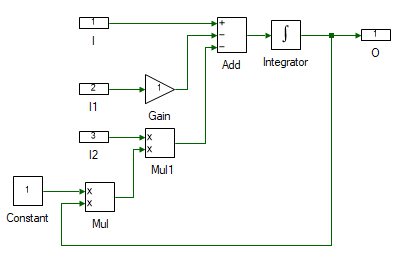
23. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    I	Name	vsdq	Stator voltage dq signal, vsdq.
    I1	Name	isdq	Stator current dq signal, isdq.
    I2	Name	wd	d-axis speed, ωd.
    Gain	Gain	IM:Rs	Stator resistance, Rr.
    Constant	Magnitude	[[0, -1], [1, 0]]	Rotational matrix
    Add	Number of ports	3
    	Add	Arithmetic operation	+--
    Integrator	Initial value	[[0], [0]]	Initial stator flux linkage.
    O	Name	fsdq	Stator dq flux, λsdq.

24. Next step is to determine the stator and rotor currents from the flux. as given in Eqn. 6 through 10. Drag and drop the tools shown and connect them as shown to implement the above equation.

    #	Tool type	Tool class	Tool name
    1	Constant	Signal Sources	Constant1
    2	Concatenation	Matrix Manipulation	Concat
    3	Concatenation	Matrix Manipulation	Concat1
    4	Constant	Signal Sources	Constant2
    5	Multiplier Divider	Math Block	Mul
    6	Decatenation	Matrix Manipulation	Decat
    7	Decatenation	Matrix Manipulation	Decat

    

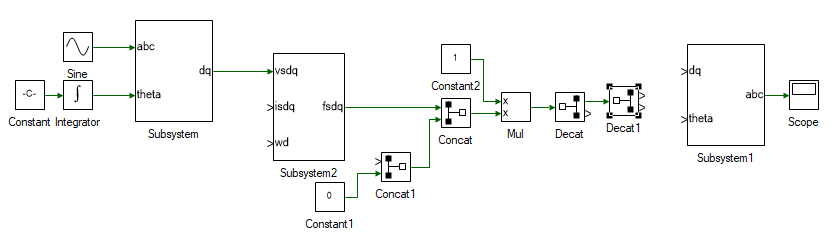
25. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    Concat	Pivot Dimension	2	Combine λsd and λsq.
    Concat1	Pivot Dimension	2	Combine λrd and λrq.
    Constant1	Magnitude	0	λrq = 0.
    Constant2	Magnitude	1/[[IM:Ls, 0, IM:Lm, 0], [0, IM:Ls, 0, IM:Lm], [IM:Lm, 0, IM:Lr, 0], [0, IM:Lm, 0, IM:Lr]]	Eqns. 6 through 10.
    Decat	Pivot Dimension	2	Split into isdq and irdq.
    Decat	Pivot Dimension	2	Split into isd and isq.

26. Next step is to determine the rotor flux and d-axis speed to close the model loop. Same as before add the following tools and connect them as shown.

    #	Tool type	Tool class	Tool name
    1	Gain	Math Block	Gain
    2	Adder Subtractor	Math Block	Add
    3	Integrator	Math Block	Integrator1
    4	Gain	Math Block	Gain1
    5	Multiplier Divider	Math Block	Mul1
    6	Multiplier Divider	Math Block	Mul2
    7	Gain	Math Block	Gain2
    8	Gain	Math Block	Gain3

    

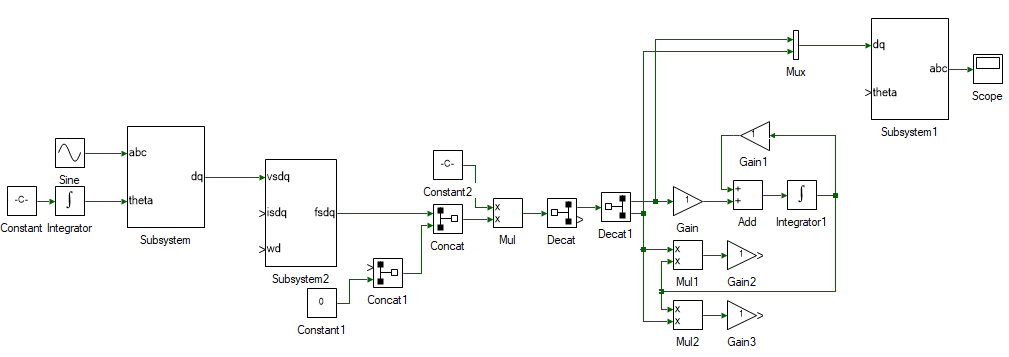
27. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    Gain	Gain	IM:Lm / IM:τr	Eqn. 14. λrd calculation.
    Add	Arithmetic operation	-+	Eqn. 14. λrd calculation.
    Gain1	Gain	1 / IM:τr	Eqn. 14. λrd calculation.
    Integrator1	Initial value	0.001	Eqn. 14. To prevent divide by zero error. Output of this is λrd.
    Mul1	Arithmetic operation	x/	Eqn. 15. ωdA calculation.
    Gain2	Gain	IM:Lm / IM:τr	Eqn. 15. ωdA calculation. Output of this is ωdA.
    Gain3	Gain	(IM:p / 2) * IM:Lm / IM:Lr	Eqn. 16. Torque caculation. Output of this is Tem.

28. The last remaining step is to determine the rotor speed using Eqn. 10. From the rotor speed and ω_dA, the rotor flux axis speed is obtained using Eqn. 11. To do this add the following tools and connect them as shown.

    #	Tool type	Tool class	Tool name
    1	Constant	Signal Sources	Constant3
    2	Adder Subtractor	Math Block	Add1
    3	Transfer function	Continuous	TransferFnc
    4	Gain	Math Block	Gain4
    5	Adder Subtractor	Math Block	Add2

    

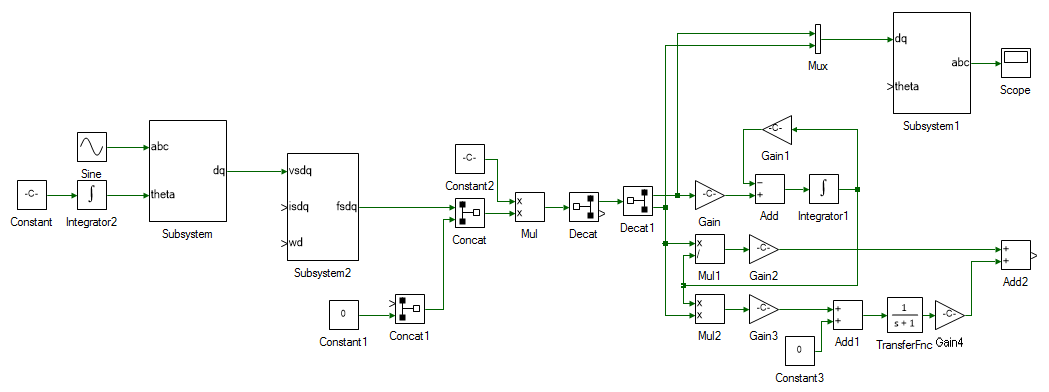
29. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    Constant3	Magnitude	0	Eqn. 10. Load torque Tl.
    Add	Arithmetic operation	+-	Eqn. 10. Tl - Tem.
    TransferFnc	Numerator	{1}	Eqn. 10 can be represented in transfer function form as (Tem - TL)/(sJ + B).
    	TransferFnc	Denominator	{IM:J, IM:B}	Eqn. 10 can be represented in transfer function form as (Tem - TL)/(sJ + B). Output of this block is the motor mechanical speed, ωmech.
    Gain5	Gain	IM:p / 2	ωm = P/2 x ωmech.
    Add2	Arithmetic operation	++	ωd = ωm + ωdA.

30. All that remains is to close the loop. Delete the Constant tool connected to the abc → dq subsystem. This was initially used as the d-axis speed and is no longer needed since we have the actual d-axis speed, aligned with rotor flux. Connect the output of Add2 which is ω_d to input of Integrator2. Output of Integrator2 is θ_da, which must be connected to dq → abc subsystem's theta input. Also connect the output of Add2, ω_d to ω_d input of stator flux subsystem. The stator dq currents for the stator flux subsystem, i_sdq is obtained by connecting the output of Decat. Finally, the rotor d-axis flux, λ`rd`, i.e. output of Integrator1 is connected to input of Concat1. The overall induction motor dq model, with d-axis aligned with rotor flux, is shown below.

    

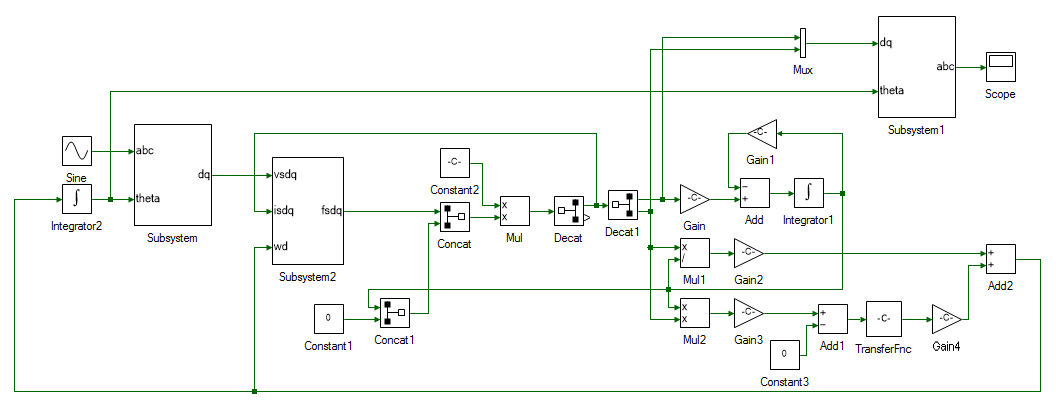
31. Set the input voltage and frequency in the Sine block.

    Tool name	Property field	Property value	Comments
    Sine	Magnitude	IM:Va	Rated peak phase voltage
    	Sine	Frequency (Hz)	IM:f	Rated frequency

32. Set the model Run time to 3.

33. Add scope to observe, abc and dq stator voltages and currents, motor speed, electromagnetic torque and any other values that might be of interest.

34. Run the simulation and observe the results.

35. Obtain results for the following operating conditions.

    1. Input frequency = 0.5 x Rated frequency, Input voltage = 1 x Rated voltage

    2. Input frequency = 1 x Rated frequency, Input voltage = 0.5 x Rated voltage

    3. Input frequency = 0.5 x Rated frequency, Input voltage = 0.5 x Rated voltage

    4. Input frequency = Rated frequency, Input voltage = Rated voltage

36. Replace the constant load torque, with a Step from Signal Sources. Set the Final value of step to 0.1 and Step time as 2.

37. Re-run the simulation and observe the results.

If any runtime exception occurs, use the DataPeek window, docked on the right, to look at each of the tool's input, output and parameter right before the exception occurred. This tool can be used to observe the value of any tool or code variables at any time. Click on the icon in the DataPeek window and select any tool to look at its value. Similarly, to look at the value of a variable in Script file, place the cursor on the variable and select it by double clicking. Its value will pop-up in the DataPeek window.

Motor current control

In this section, the current through the motor is controlled using a PI controller.

1. Compute the k_i,p and k_i,i using Eqns. 28 through 30 for the system to have phase margin Φ_i = π/3 at cross-over frequency ω_i,c = 2π x 200. The cross-over frequency is chosen as 200 Hz, which is < 1/10ᵗʰ the switching frequency of 6 kHz. This is merely a thumb rule, where every additional loop is 1/10ᵗʰ or less than the bandwidth of inner loop. In this case, it helps prevent the current controller from trying to compensate the switching current harmonics.

2. Open a new instance of Workbench.

3. In the motor model designed earlier, the motor currents and the speed are determined based on applied terminal voltage and load torque. These two parameters are measured using current and speed sensors for sensored-vector control. From these two parameters the rotor flux position is established using Eqn. 11 and 15 as already implemented earlier within the motor model. The control voltages are generated in dq frame and this must be converter to abc voltages to be generated by the power processing unit. This dq-abc transformation has been implemented earlier as well.

   These two blocks are already implemented and can be opened from the examples folder usually in C:\Program Files (x86)\Sciamble\WorkBench v1\Examples\CUSPLab\AdvancedDrives\Experiment4\CurrentController. This motor model subsystem is the model that was built in the previous section and has been enclosed within a subsystem. In addition, the abc-dq transformation and the estimator subsystem have been added to the model file.

   

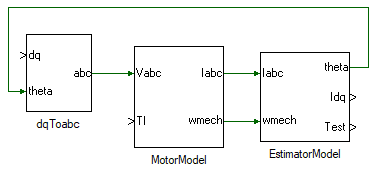
4. Add another subsystem to the model, where the d-axis PI current controller will be modelled. Double click and open the subsystem.

5. Drag and drop the following tools from the Toolbox to the subsystem model and connect them as shown.

   #	Tool type	Tool class	Tool name
   1	In-port	Signal Routing	I
   2	In-port	Signal Routing	I1
   3	Adder Subtractor	Math Block	Add
   4	Gain	Math Block	Gain
   5	Gain	Math Block	Gain1
   6	Integrator	Math Block	Integrator
   7	Adder Subtractor	Math Block	Add2
   8	Saturation	Non-linear	Saturation
   9	Out-port	Signal Routing	O

   

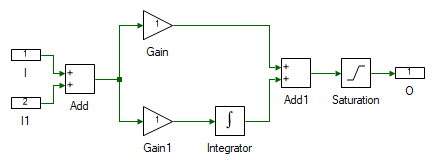
6. Change the properties of each tool to values listed in table below.

   Tool name	Property field	Property value	Comments
   I	Name	Ref	Desired reference motor current.
   I1	Name	Fbk	Actual motor current.
   Add	Arithmetic operation	+-	Difference between the desired and actual motor current.
   Gain	Gain	ki,p	Substitute the value of ki,p computed in step 1.
   Gain1	Gain	ki,i	Substitute the value of ki,i computed in step 1.
   Integrator	Integrator Type	Anti-windup	Reason explained later.
   	Integrator	Upper Limit	20
   	Integrator	Lower Limit	-20
   Saturation	Upper Limit	20
   	Saturation	Lower Limit	-20
   O	Name	Out	Applied terminal voltage to generate the desired current profile.

   When there is a large difference between the desired current and the actual current, the PI controller produces a large output voltage to quickly correct this error. In real-world, the magnitude of this voltage is limited either due to available DC bus voltage or due to motor and power electronics voltage ratings. Hence in practical implementation of PI controller, the output of the PI controller is saturated to the maximum possible voltage. So, during transient conditions, when the actual current is different from the desired current, the Integrator in the PI controller rapidly builds up its output to a large value due to persistent input error. When the error does goes back to zero, this large output built up by the integrator does not die down and cause the actual current to overshoot the desired the value, causing the error to go negative, which causes the integrator output to fall, but it will end up falling by much larger value than desired causing the current to undershoot. This keeps repeating, and this oscillation will die down slowly. To avoid this, the value up to which integrator is active is clamped by setting it to Anti-windup. If the integrator output reaches this value, the integrator is disabled until the polarity of the error reverses. This improves the response of the system significantly.

7. Create a copy of the PI subsystem for q-axis current control. Connect the output of these two PI controllers to the dq to abc subsystem as shown:

   

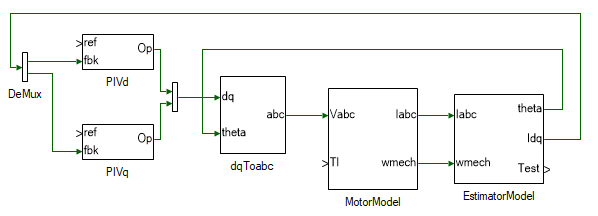
8. Set the d-axis current reference to a constant obtained by solving Eqns. 17 through 21.

9. Set the q-axis current reference to step from 0 A to 1 A at time t = 2s.

10. Add a step load torque and for the time being set the Final value to 0.

11. Run the simulation and observe if the steady state dq currents match the reference currents as well if the transient response is satisfactory.

Motor speed control

In this section, the speed of the motor is controlled using a PI controller.

1. Compute the k_s,p and k_s,i using Eqn. 14 through 17 for the system to have phase margin Φ_s = π/3 at cross-over frequency ω_s,c = ω_i,i/10 = 2π x 20. The cross-over frequency is chosen as 20 Hz, which is 1/10ᵗʰ the cross-over frequency of inner current loop.

2. Replace the step source for q-axis current reference with a PI controller subsystem, output of which will be the reference q-axis current.

3. Change the PI gains to the values computed in the earlier step. Saturate the integrator and the PI subsystem's output to 5, which is the transient current limit of the motor under test.

4. Connect the feedback input to motor speed from the motor model subsystem. Apply a step speed for reference, stepping from 0 to 100 rads/s at time t = 2s.

5. Change the Final value of load torque to 0.05 Nm at time t = 4 s.

6. Run the simulation and observer if motor steady state speed matches the reference speed.

This concludes the simulation of induction motor vector control. In the following section, a pre-built induction motor vector control model is run in real-time.

Real-time vector control of Induction motor

1. Open Workbench and pin the Explorer and Properties dock.

2. Navigate to and open the IMVectorControl project file in Experiment4\Realtime folder usually in the following location: C:\Program Files (x86)\Sciamble\WorkBench v1\Examples\CUSPLab\AdvancedDrives.

3. Expand the project in the Explorer and open the ModelFile model file shown below:

   

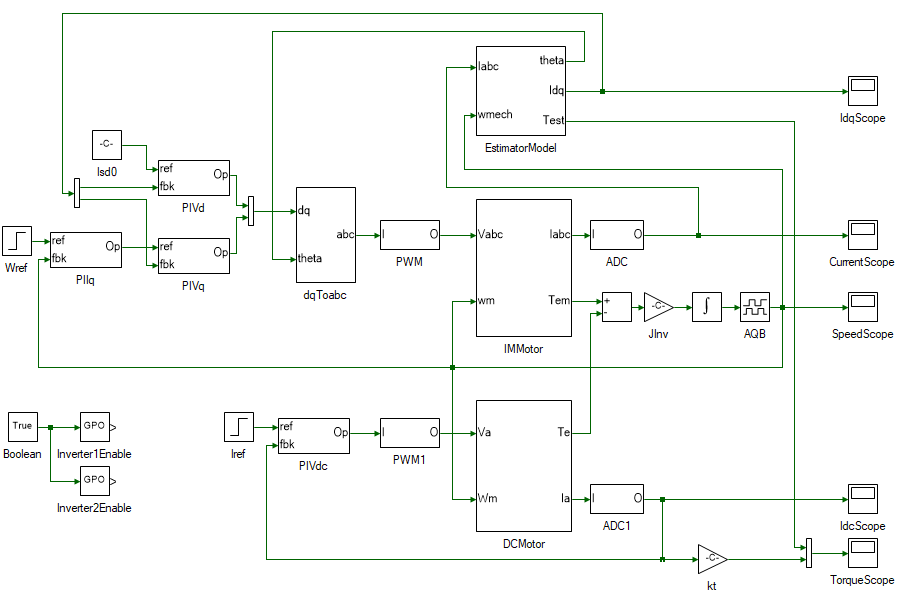
   The top section of the model consists of the induction motor vector control and is merely a replication of the simulation model developed earlier with few additions to enable real-time control. On the left is the speed PI controller, followed by the d and q axis current PI controller, the output of which is the dq terminal voltages. The dq voltages are converted to abc voltages in the following subsystem. In the simulation model, this terminal voltage signal was connected to the motor model. In this case it is converted to inverter's PWM duty cycles, to control the PMAC motor in real-time. In real-time mode, the stator currents are measured from the actual motor currents by means of ADCs and these are on the top-right corner of the model. The speed is measured from the actual motor's A-quad-B encoder. In simulation the rotor position is obtained by integrating the rotor speed. In real-time this is obtained from AQB position toolbox. The speed itself in real-time is obtained by actually differentiating the AQB position value. Hence integrating speed to obtain position will lead to loss of precision compared to just directly reading the position.

   The bottom section consists of the DC motor current control. This is used to emulate the load torque.

4. The Init() function within the IMParam script file computes the controller parameters based on the motor parameters, and the loop cross-over frequency and phase margin. Set the speed loop cross-over frequency ωc and the phase margin φm in the script to the same value used in simulation.

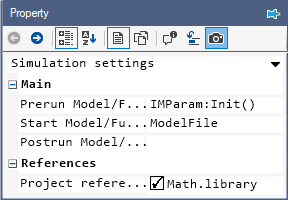
5. The Init() function must be called prior to running the simulation model to initialize the controller gain values. To do this open project properties, double click on the IMVectorControl project node in the Explorer, and set the Prerun Model/Function to IMParam:Init() as shown below:

   Similarly set the Start model/Function to ModelFile, to run the model after parameter initialization.

   

6. Click the button to run the model in simulation mode. Using the DataPeek, verify that the controller gain parameters computed by the Init() function matches that of values computed earlier.

7. Turn ON the DC power supply and set the voltage to 40 V.

8. Ensure that button on the top dock, to transition to real-time mode, is pressed. Click the run button.

   Note

   When the real-time mode button is pressed, the motor model gets grayed out. Tools that are grayed out indicate that they are not coded in real-time. Workbench can automatically identify tools that need to be coded in real-time and those that dont. This allows for using a single unified model for both real-time as well as simulation which generating a highly optimized real-time code.

9. Observe the speed and current result in the scope. Click the to focus the result. After about 5 s, stop data logging by clicking .

10. Turn OFF the DC power supply.

11. If necessary, repeat the experiment for different loop cross-over frequencies and phase margins.

12. Turn OFF the DC power supply and disconnect all the connections including the USB.

Lab report and reading assignment

1. List the k_p and k_i values of the current and speed PI controller.

2. Attach the plot of 3φ stator and rotor currents from simulation.

3. Attach the plot of the electromagnetic torque response, stator dq current, and the rotor speed from both simulation and real-time.

4. Ignoring the noise in the waveform in real-time mode, do the stator dq currents and the electromagnetic torque waveforms match those obtained from simulation? If not, explain why.

5. Read through and add comments to each line of code in the Init() function. Later experiments would require writing the script file to compute the controller parameters.

Reference

1. "Analysis and Control of Electric Drives: Simulations and Laboratory Implementation," Ned Mohan and Siddharth Raju, Wiley Publication.