Characterization of DC motor

• August 03, 2019
• 2 hours to complete
• Workbench v1.5
• • 
  • 

Introduction

A DC motor can be mathematically modeled as an electrical system and a mechanical system, tied together by relationship between back-emf and speed, and relationship between current and torque. In this experiment, the electrical and mechanical parameters of the DC motor are determined. These values are necessary to design a proper control system to control motor speed, torque, or position as will be seen in later experiments.

Theoretical background

Motor model

The DC motor like all real-world systems, exhibits non-linear behavior. In the model shown below, a linearized DC motor model is considered for the sake of design simplicity. It will be verified in later experiments that the results from the simulated linearized model closely matches the real-world model thus validating this approximation.

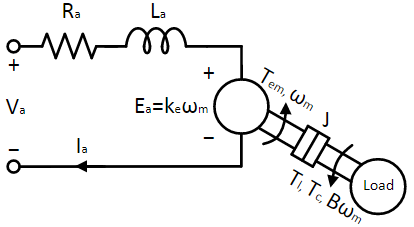
In a permanent magnet DC motor, such as the one used in this experiment, the stator contains the permanent magnet and the rotor contains the armature winding. When current flows through the armature winding, it generates flux, which interacts with the magnetic field established by the permanent magnet, and this interaction generates an electromagnetic torque, T_em which rotates or stalls the motor. The torque T_em is proportional to the armature current I_a as given in Eqn. 1 where k_T is the torque constant.

T_em = k_t × I_a(1)

As the motor rotates, the armature winding cuts through the magnetic field which induces the back emf, E_a on the armature winding. When the motor rotates faster, the rate of change of magnetic flux dϕ/dt increases, proportional to the rotor speed. This is given by Eqn. 2 where ω_m is the motor speed and k_e is the back-emf constant.

E_a = k_e × ω_m(2)

The power needed to drive the motor is given by the E_a × I_a. The mechanical power needed to drive the motor is given by T_em × ω_m. Since these two quantities are one and the same (in SI units), from Eqn. 1 and 2, k_t = k_e. R_a and L_a in the above model refers to the armature resistance and inductance respectively. The voltage applied at the terminal V_a equals the sum of voltage across the passive elements - R_a and L_a, and the back-emf E_a. This represents the electrical model of the DC motor and is given in Eqn. 3, where E_a has been replaced with k_e × ω_m from Eqn. 2.

V_a = R_aI_a + L_adI_adt + k_eω_m(3)

The mechanical model of the DC motor is given in Eqn. 4. Under steady state, the torque generated by the motor T_em equals the sum of load torque T_l and the torque necessary to compensate the frictional losses, T_fric. In transient condition when T_em ≠ T_l + T_fric, the motor accelerates if the former is greater than the latter, storing the excess energy as inertial energy. It decelerates if the former is less than the latter, loosing previously stored inertial energy. The motor inertia is identified as J in Eqn. 4.

T_em = T_l + T_fric + Jdω_mdt(4)

The frictional component is due to various factors and is always against the direction of rotation. Of the many causes, only Coulomb friction which is a constant and viscous friction which varies proportionately with rotational speed are considered, since these are the ones that have significant effect on the steady-state. The torque associated with Coulomb friction is given by T_c and that of viscous friction is given by B × ω_m, where B is the coefficient of viscous friction. Substituting these into Eqn. 4 yields the final mechanical model as given in Eqn. 5.

T_em = T_l + T_c + Bω_m + Jdω_mdt(5)

Parameter estimation

In this experiment, the electrical model parameters, R_a, L_a, k_e and, the mechanical model parameters, T_c, B and J, are determined for the DC motor as follows:

1. R_a: Use a multimeter. Alternatively, lock the rotor such that it does not rotate and apply a constant voltage, V_a of less than 2 V at the motor terminal and measure the steady-state motor current I_a. Divide V_a by I_a to obtain the armature resistance R_a. Locking the rotor eliminates the back-emf component in Eqn. 3, and the steady-state current eliminates the drop across armature inductance L_a. Thus, all the applied terminal voltage is dropped solely across the armature resistance.

2. L_a: Like before, the rotor is locked to prevent it from rotating to eliminate the back-emf component in Eqn. 2. The equation becomes:

   V_a = R_aI_a + L_adI_adt(6)

   When a step voltage of magnitude V at time t = t_step, is applied to the motor terminals, the solution to above equation for current I_a is given in Eqn. 7. The value of differential of Eqn. 7 evaluated at t = t_step is given in Eqn. 8. Rearranging Eqn. 8, armature inductance can be obtained, as given in Eqn. 9.

   I_a = V_aR_a(1 - e^-tR_a/L_a)(7)

   dI_adt(t_step) = I_a'(t_step) = V_a(t_step)L_a(8)

   L_a = V_a(t_step)I_a'(t_step)(9)

3. k_e = k_t: There are two ways to identify k_e, first using just a coupled motor-generator set, and the other using single motor. In the former, run the generator at constant speed while the motor terminals are left open. Measure the motor/generator speed ω_m and the motor back-emf E_a which is same as the motor terminal voltage V_o since it is open. From these two measurements, k_e can be determined by using Eqn. 2.

   Alternatively, if only a single motor is used, apply a constant voltage V_o at the motor terminal. Measure the motor current I_a and motor speed ω_m at steady-state. Compute k_e from Eqn. 10, which is obtained from Eqn. 3 where the drop across inductance L_a is zero under steady-state condition because I_a is a constant.

   k_e = V_a - R_aI_aω_m(10)

   The second method is used in this experiment since the same method is used to estimate frictional components as well as highlighted in the next step.

4. T_c and B: If the motor is not accelerating i.e. motor speed is a constant, and there is no load connected, the inertial torque component and load torque component in Eqn. 5 becomes zero, leading to the following equation:

   T_em = T_c + Bω_m(11)

   Apply a constant voltage V_o, at the motor terminal. Measure the motor speed ω_m, and current I_a. The electromagnetic torque T_em can be computed from the measured current I_a using Eqn. 1. Repeat the same for different voltages and plot the result, T_em (y-axis) vs. ω_m (x-axis). The resulting plot will be linear. The slope of the plot equals the coefficient of viscous friction B and the y-axis intercept is the frictional torque T_c, due to Coulomb friction.

5. J: Apply a constant voltage V_o, at the motor terminal. Once the speed settles down, measure the speed ω_m, and motor current I_a. At steady state, the electromagnetic torque T_em (Eqn. 1), solely compensates for drag due to friction. Disable the inverter so that the motor current dies-down to zero rapidly. After this, there is no electromagnetic torque and all the frictional losses must be supplied from the inertial energy. This leads to the motor to stop gradually. This is summarized in Eqn. 12, which is obtained by equating T_em and load torque T_l in Eqn. 4 to zero.

   0 = T_fric + Jdω_mdt(12)

   At the moment the inverter is disabled, time t = T_dis, the frictional torque component T_fric is same as, that of electromagnetic T_em just before disabling the inverter, which can be obtained from the steady-state current I_a before disabling the inverter using Eqn. 1. Substituting this into Eqn. 12 yields:

   J = k_e×I_a(T_dis)dω_mdt(T_dis)(13)

   Thus, the motor inertia can be obtained by dividing, the electromagnetic torque just before disabling the inverter, with the motor deceleration just after disabling the inverter.
   Note

   Disabling the inverter is not the same as setting the output voltage to 0. In the former, the motor current extinguishes at a rate much faster than the slowdown of the motor speed. After this point, the inertial energy is not lost to the armature resistance or to the source. If the terminal voltage was set to zero, the inertial energy in addition to being lost in friction, will also be lost in the armature resistance because the back-emf will source the current due to the terminal being effectively shorted.

Real-time parameter estimation

1. R_a: Measure across the motor terminal using a multimeter.

2. L_a:

   1. Open Workbench and pin the Explorer and Properties dock.

   2. Navigate to and open the DCMotor project file in Experiment3 folder usually found in the following location: C:\Program Files (x86)\Sciamble\WorkBench v1\Examples\CUSPLab\BasicDrives.

   3. Expand the project and open the LsEstimate model file (double clicking on the model node). Open the model properties (double click anywhere in the blank space of the open model). Copy the value in the property labelled Name, which if previously unchanged will be LsEstimate.

   4. Since this project has more than one model file, the project must be notified as to which of these models should be run. To do this, open the project properties (double click on the project node in the Explorer dock) and paste the copied model name (LsEstimate) into the Start model/Function field.

   5. Shown below is the LsEstimate model:

      

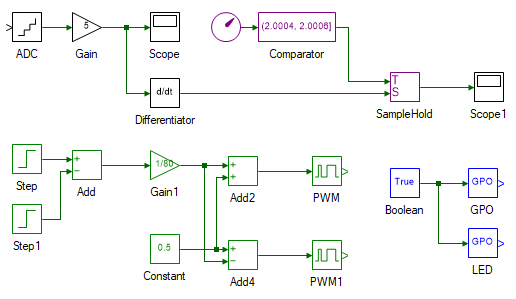
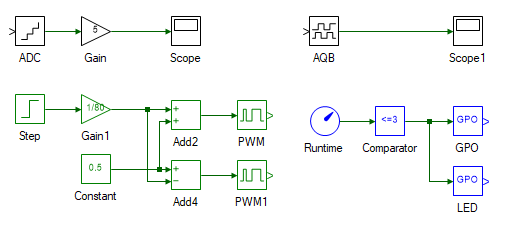
      The GPO tool, in components highlighted in blue on the bottom right corner, is the Inverter 1 enable pin and is set to ON (True). The LED tool, in that same section, is the green LED on the side of the three inverter, right next to the red power LED. This is just an indicator that glows when the code begins to execute. The tools highlighted in green, represents the inverter PWM generation logic, as seen in the previous experiment. For estimating inductance, the rotor must not rotate. Since it is rather difficult to physically lock the rotor from rotating, we instead excite it for a brief period. The excitation pulse is applied at time t = 2 s, and has a magnitude of 40 V and time period of 1 ms. In this brief interval, the motor does not develop sufficient electromagnetic torque to counteract the static friction and hence the speed remains at zero, having the same effect as locking the rotor.

      As per above discussion, the terminal voltage V_o and the current differential I'_a, at time t = 2 s i.e. right after exciting the armature winding, is needed for estimating L_a. The simulation model is run at a step time of 0.2 ms. Even though this update rate is good enough for observing I'_a, the rate at which the data itself is logged is much slower. Data from each evaluation is not logged on to the computer due to limited data transfer bandwidth. Hence simply adding a scope to observe I'_a will in most cases not capture the data at the exact instant needed. This limitation is overcome by the blocks shown in purple. These capture the I'_a in the short time between 2.0004 and 2.0006 s, right after exciting the motor and holds on to it using a sample-and-hold block, which ensures that the sampled data is definitely logged to the scope.

      Finally, in the blocks highlighted in black, the ADC block represents the motor current feedback. Double click on it to observe its properties and make note of the property labelled Signal Scaling. The inverse of this value represents the factor by which the ADC output must be scaled to obtain the actual current. The Gain block following the ADC block does this scaling.

   6. Connect the motor (the one without the encoder) to Inverter 1 (color of the motor terminal must match that of the inverter's). Even though the generator (the one with encoder) is not used in this case, connect it to Inverter 2 instead of leaving the terminals open (once again the color of the motor terminal must match that of the inverter's).

      Connect the three-inverter module to the DC power supply. Connect the three-inverter to the computer via USB. Connect the generator speed feedback to the three-inverter's Encoder 1 DSUB connector in the back panel.

   7. Turn ON the DC power supply and set the voltage to 40 V.

   8. Ensure that button on the top dock, to transition to real-time mode, is pressed. Click the run button.

   9. Open the scope (double click) named Scope1 to see the data log of I_a differential. After about 5 s, when a step change in the plot is observed, stop the data logging by clicking on button. Auto-focus the scope result by clicking in the Scope's toolbar. The result should look like the waveform shown below:

      

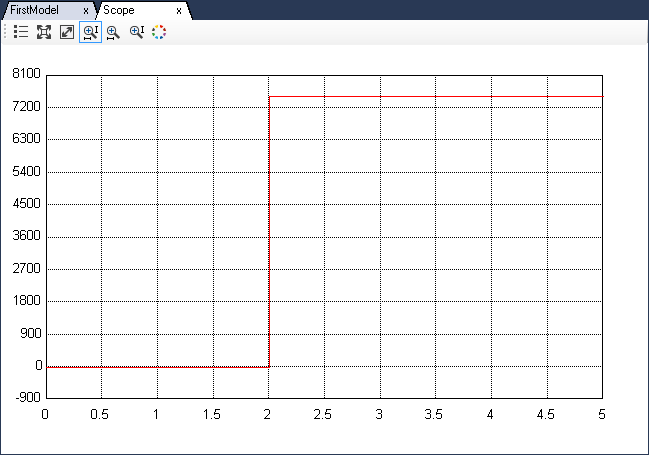
   10. Zoom in and make a note of the plot's peak which is, the I_a differential immediately after the application of voltage pulse to the motor.

       Repeat the previous 2 steps to get at least 5 different readings.

   11. Compute the value of L_a for each of the reading using Eqn. 9, where V_a(t_step) = 40 V.

       Motor armature inductance L_a is the average of the above samples.

   12. Close the LsEstimate model.

3. k_e = k_t, T_c and B:

   All the three parameters are estimated using the same method, in this step.

   1. Open the keEstimate model within the same project.

   2. Open the model properties (double click on the blank-space) and copy the property Name.

   3. Go to project properties (double click on project node) and set the Start model/Function to the copied value.

   4. The model is shown below. The motor is given a constant step voltage and the motor current and speed are measured.

      

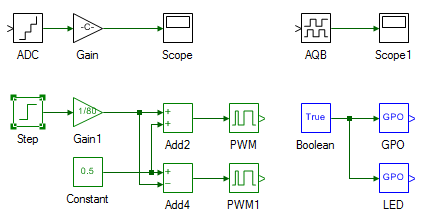
   5. Open Step tool's properties and set the Final value property to 10.

   6. Ensure that the motor is connected as done while estimating L_a and that the DC power supply is turned ON with voltage of 40 V.

      Click followed by to run the model in real-time.

   7. After about 5 s, when Scope1 has logged the data, click to stop data logging.

      Note

      The motor will continue to run since only data logging was halted.

   8. Make note of the results in a table of following layout:

      Va (V)	Ia (A)	ωm (rads/s)	ke	Tem (Nm)

      where, V_a is the motor terminal voltage which can be obtained from the Final value property of Step block, I_a is the motor current logged in Scope, and ω_m is the motor speed logged in Scope1. All these values must be measured after reaching steady-state after applying the desired voltage. The remaining table entries are computed based on these values and will be explained in the following steps.

   9. Repeat the previous three steps for different motor terminal voltages, from 10 V to 20 V, in steps of 2 V. The voltage can be changed by changing the Step tool's Final value property.

   10. Turn OFF the DC power supply and unplug the USB cable.

   11. From the above table, k_e, which is equal to k_t, is computed using Eqn. 10. The final k_e is the average of all the computed values.

   12. Using the average k_t, compute T_em for each I_a. Plot the result of T_em (y-axis) vs ω_m (x-axis).

       Measure the slope of the get an estimate of coefficient of viscous friction B and the y-axis intercept to get the frictional torque due to Coulomb friction T_c.

   13. Close the keEstimate model.

4. J:

   1. Open the JEstimate model within the same project.

   2. Open the model properties (double click on the blank-space) and copy the property Name.

   3. Go to project properties (double click on project node) and set the Start model/Function to the copied value.

   4. The model is shown below. The motor is given a step voltage of 25 V (Step's Final value property) at time t = 1 s. When the motor has reached its steady-state, the inverter is disabled at t = 3 s. This puts the inverter terminals at high-impedance so that, the inertial energy is lost only in the frictional component.

      

   5. Re-connect the USB and turn on the DC power supply.

   6. Ensure that is pressed. Click to run the model in real-time.

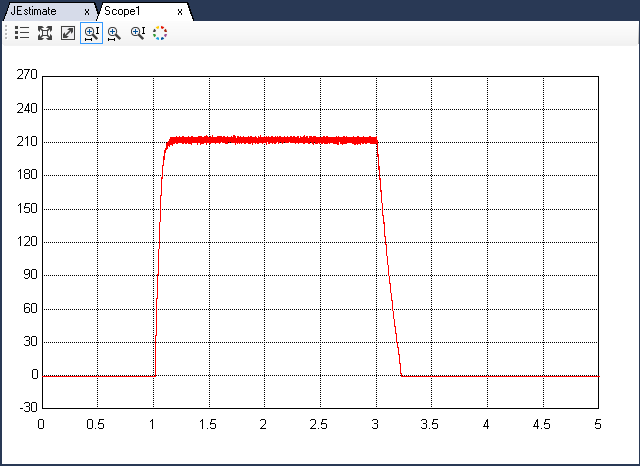
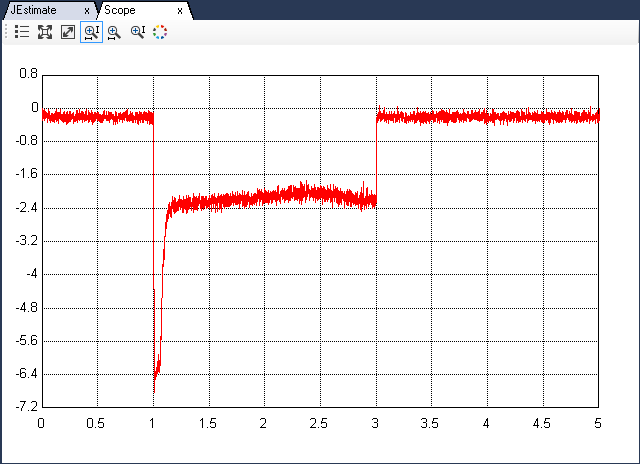
   7. Open the scope Scope1 to observe the motor speed. When the data has been logged for 5 s, click the to stop the data logging. The results in Scope and Scope1 will look like this:

      

      

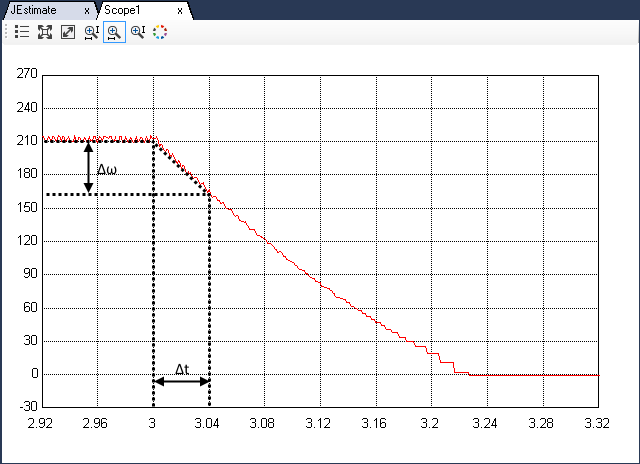
   8. Zoom in on the speed at t = 3s and determine the slope as shown below.

      

      In the current's plot, make note of the current's magnitude, before the inverter was disabled at t = 3 s.

   9. Calculate inertia J, using Eqn. 13.

5. Turn OFF the DC power supply and disconnect all the connections including the USB.

This concludes the experiment on DC motor characterization. The parameters estimated in this experiment will be used in the following experiments, to tune a PI loop to control the motor speed.

Lab report and reading assignment

1. Attach plot of I'_o from L_a estimation.

2. Attach plots of I_o and ω_m for different V_o from k_e estimation.

3. Attach plot of I_o and ω_m from J estimation.

4. Attach the table from k_e estimation.

5. List the results of all final parameter values.