DC motor speed control

• August 03, 2019
• 2 hours to complete
• Workbench v1.5
• • 
  • 

Introduction

In this experiment, a mathematical model of a permanent magnet DC motor will be simulated based on the parameters estimated in the previous experiment. It will be shown that the motor speed cannot be held a constant under varying load and voltage conditions. To overcome this, a closed loop system will be developed using a PI controller so that the output speed closely matches the desired speed under various load conditions. Finally, the designed system will be run in real-time to control the actual DC motor at constant speed.

Theoretical background

Motor model

The DC motor model characterized in previous experiment is summarized in Eqns. 1 through 4, in transfer function form:

I_a = V_a - E_asL_a + R_a(1)

T_em = k_tI_a(2)

ω_m = T_em - T_l - T_csJ + B(3)

E_a = k_eω_m(4)

where

1. V_a : terminal voltage

2. E_a : back-emf

3. I_a : armature current

4. R_a : armature resistance

5. L_a : armature inductance

6. k_e : back-emf constant

7. k_t : torque constant

8. J : rotor inertia

9. B : coefficient of viscous friction

10. T_c : torque due to Coulomb friction

11. T_em : output/electromagnetic torque

12. T_l : load torque

13. ω_m : rotor speed

Based on the application, the motor output torque, speed or position may need to be controlled. In the following section, a PI controller is designed to control the motor output torque by controlling the terminal voltage applied.

Controller Design

Consider the scenario where the motor's output/electromagnetic torque needs to controlled. Eqn. 2 shows that this can be directly achieved by controlling the motor armature current. This is achieved by means of a PI (Proportional-Integral) controller whose transfer is given in Eqn. 5 where, k_i,p and k_i,i are the proportional and integral gains respectively. The input to this controller E, is the difference between the desired armature current I_ref and actual armature current I_a, as shown in Eqn. 6. Output of this controller is the armature voltage that must be applied to get the desired armature current and in turn the desired motor output torque.

PI(s) = V_a(s)E(s) = k_i,p + k_i,is(5)

E(s) = I_ref(s) - I_a(s)(6)

The current control system is summarized as shown below, where M(s) is the actual motor model:

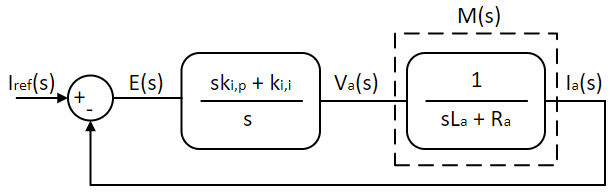
For a small change in PI controller error signal, the proportional change in current, obtained from Eqns. 1, 5, and 6, is given below:

ΔV_a(s) = (k_i,p + k_i,is) × ΔE(s)(7)

ΔI_a(s) = ΔV_a(s)sL_a + R_a(8)

The back-emf term has been ignored in the above small signal model because, when V_a changes, I_a changes at a rate much faster than E_a. This is because, the mechanical time constant of the motor, given by J/B, is much larger than the electrical time constant, given by L_a/R_a. Since the back emf is proportional to the rotor speed, it changes at a rate slower than the armature current can, to a step change in applied voltage and hence, it is justifiably ignored in the above equation. The overall small signal model is obtained by combining the above two equations.

ΔI_a(s)ΔE(s) = k_i,ps + k_i,is × 1L_as + R_a(9)

The k_i,p and k_i,i gain values are adjusted to have the desired transient response. There are multiple ways to quantify the desired response. In time domain, usually the desired rise time and overshoot for a step input is mentioned and the gains are adjusted to satisfy this requirement. Alternatively, in frequency domain, the desired phase margin and cross-over frequency are mentioned. We shall go the latter route since it gives a better picture of the system stability. The steady state response of the system is obtained by replacing s = jω in Eqn. 9.

ΔI_a(jω)ΔE(jω) = G(jω) = jωk_i,p + k_i,ijω × 1jωL_a + R_a(10)

The above system is tuned for a desired phase margin of Φ_i at cross-over frequency ω_i,c as follows. At the cross-over frequency, the system gain equals 1 and the system phase shift equals -π + Φ_i. Substituting this into Eqn. 10:

∠G(jω_i,c) = -π + Φ_i = -π2 + tan^-1(ω_i,ck_i,pk_i,i) - tan^-1(ω_i,cL_aR_a)

⇒ ω_i,ck_i,pk_i,i = tan(Φ_i - π2 + tan^-1(ω_i,cL_aR_a))

⇒ k_i,p = k_i,iω_i,c × tan(Φ_i - π2 + tan^-1(ω_i,cL_aR_a)) = C1 × k_i,i(11)

where,

C1 = 1ω_i,c × tan(Φ_i - π2 + tan^-1(ω_i,cL_aR_a))(12)

and

|G(jω_i,c)| = 1 = |jω_i,ck_i,p + k_i,ijω_i,c × 1jω_i,cL_a + R_a|

⇒ (ω_i,ck_i,p)² + k²_i,i = ω²_i,c((ω_i,cL_a)² + R²_a)

⇒ k²_i,i= ω²_i,c × (ω_i,cL_a)² + R²_a(ω_i,c × C1)² + 1(13)

Given the desired Φ_i and ω_i,c, and the motor parameters, the PI gains can be solved using Eqns. 11 through 13.

The above controller maintains the motor at desired current and in turn the desired motor torque, while other system inputs vary. To achieve speed control as opposed to torque control, the above system is modified by adding an outer speed PI controller to the existing inner current PI controller as shown below:

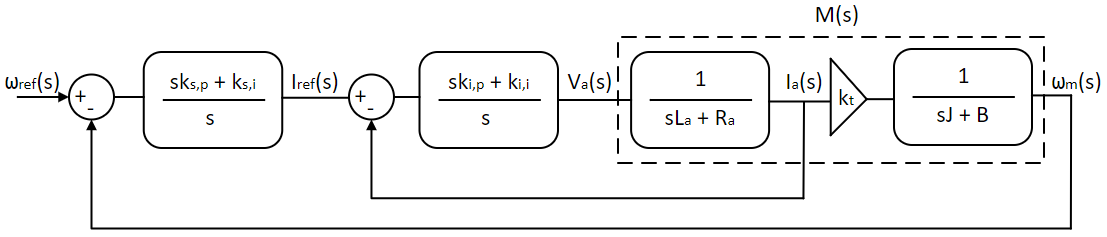
where, M(s) is the actual motor model and I(s) is the current-controlled system model which includes the current PI controller and motor model of armature current.

To control the speed of the motor as opposed to the torque, the same procedure can be followed with the following simplifying assumption, i.e. the response time of motor current is an order of magnitude smaller than that of the response time of motor speed for a step change in applied voltage. This is achieved by making the cross-over frequency, which is also the system bandwidth in this case, of the current loop PI controller to be an order of magnitude higher than that of the speed loop PI controller. So, for a step change in applied voltage, the current reaches its final steady state much earlier than the motor speed does. Thus, for tuning the speed controller, I(s) in the above figure can be assumed to be 1. The simplified speed controller model is shown below:

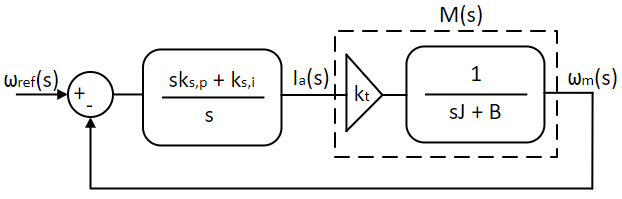
From Eqns. 2 and 3, for a small change is motor current, the change in motor speed is given by:

Δω_m(s)ΔI_a(s) = k_s,ps + k_s,is × k_tJs + B(14)

The above system is similar to that of the current controller designed earlier and going through the same procedure, the speed controller's gains are obtained to be:

k_s,p = C2 × k_s,i(15)

where,

C2 = 1ω_s,c × tan(Φ_s - π2 + tan^-1(ω_s,cJB))(16)

and

k²_s,i= (ω_s,ck_t)² × (ω_s,cJ)² + B²(ω_s,c × C2)² + 1(17)

where, k_s,p and k_s,i are the speed Pi controller's proportional and integral gain.

Simulation of DC motor speed control

The above speed control model is simulated using Workbench in this section.

Open loop motor model

1. Create a new project and add a new model file to the project.

2. Set this model file as the Start model/Function in project properties.

3. Open model properties and set the Step time to 1E-4.

4. Drag and drop a subsystem tool from the Toolbox which is present in Signal Routing tool class.

5. Subsystem is merely an enclosure within which more tools can be added. Double click the subsystem to open it.

6. Drag and drop the following tools from the Toolbox to the subsystem model and connect them as shown.

   #	Tool type	Tool class	Tool name
   1	In-port	Signal Routing	I
   2	Adder Subtractor	Math Block	Add
   3	Transfer Function	Continuous	TransferFnc
   4	Out-port	Signal Routing	O
   5	Gain	Math Block	Gain
   6	In-port	Signal Routing	I1
   7	Adder Subtractor	Math Block	Add1
   8	Transfer Function	Continuous	TransferFnc1
   9	Gain	Math Block	Gain1
   10	Out-port	Signal Routing	O1

   

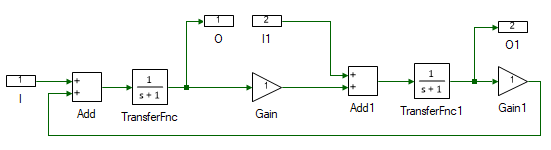
7. Change the properties of each tool to values listed in table below. Reason for each of those values are mentioned in the right-most column.

   Tool name	Property field	Property value	Comments
   I	Name	Va	Motor applied terminal voltage Va
   Add	Arithmetic operation	+-	Computes Va - Ea in Eqn. 1
   TransferFnc	Numerator	{1}	Numerator of transfer function in Eqn. 1 which is equal to 1.
   	TransferFnc	Denominator	{La, Ra}	Denominator of transfer function in Eqn. 1. Substitute the values for La and Ra obtained from previous experiment. The output of this tool is the motor current.
   O	Name	Ia	This is the motor current.
   Gain	Gain	kt	Substitute the value of kt = ke obtained from previous experiment. The output of this tool is Tem as given by Eqn. 2.
   I1	Name	Tl	Load torque
   Add1	Arithmetic operation	-+	The differential torque in Eqn. 3 is the output of this tool which computes Tem - Tl. For this model Tc is ignored but may be subtracted as well if wanted.
   TransferFnc1	Numerator	{1}	Numerator of transfer function in Eqn. 3 which is equal to 1.
   	TransferFnc	Denominator	{J, B}	Denominator of transfer function in Eqn. 3. Subtitute the values for J and B obtained from previous experiment. The output of this tool is the motor speed.
   Gain1	Gain	ke	The motor speed is scaled by ke to obtain back-emf Ea. This is looped back to Add to get the voltage difference.
   O1	Name	wm	This is the motor speed ωm.

8. Go back to the main motor model by clicking on the tab on the top.

9. Resize the subsystem so that all the ports can be seen. A tool can be resized by clicking and dragging any of the four squares in the tool's corner.

10. To observe the motor speed and current when a voltage and load is applied to the motor, add the following tools and connect them as shown, to the main model.

    #	Tool type	Tool class	Tool name
    1	Step	Signal Sources	Step
    2	Step	Signal Sources	Step1
    3	Mag-time Scope	Display	Scope
    4	Mag-time Scope	Display	Scope1

    

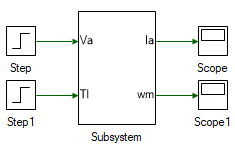
11. Change the properties of each tool to values listed in table below.

    Tool name	Property field	Property value	Comments
    Step	Final value	10	Start at 0 V and step the applied voltage to 10 V
    	Step	Step time	1	Step the voltage at time t = 1 s
    Step1	Final value	0.05	Start at 0 Nm and step the load torque to 0.05 Nm
    	Step1	Step time	7	Step the load at time t = 7 s

12. Run the simulation model and observe the current and speed result in the scope. As can be seen, the current and speed both change when either applied voltage or the load torque is varied. In the following steps the PI controller designed earlier is added to control the motor current and speed profile.

Motor current control

In this section, the current through the motor is controlled using a PI controller.

1. Compute the k_i,p and k_i,i using Eqns. 11 through 13 (first compute C1 using Eqn. 12, then k_i,i using Eqn. 13 and finally k_i,p using Eqn. 11) for the system to have phase margin Φ_i = π/3 at cross-over frequency ω_i,c = 2π x 600. The cross-over frequency is chosen as 600 Hz, which is 1/10ᵗʰ the switching frequency of 6 kHz. This is merely a thumb rule, where every additional loop is 1/10ᵗʰ the bandwidth of inner loop. In this case, it helps prevent the current controller from trying to compensate the switching current harmonics.

2. Delete Step tool connected to the V_a port of the motor model.

3. Add another subsystem to the model, where the PI controller will be modelled. Double click and open the subsystem.

4. Drag and drop the following tools from the Toolbox to the subsystem model and connect them as shown.

   #	Tool type	Tool class	Tool name
   1	In-port	Signal Routing	I
   2	In-port	Signal Routing	I1
   3	Adder Subtractor	Math Block	Add
   4	Gain	Math Block	Gain
   5	Gain	Math Block	Gain1
   6	Integrator	Math Block	Integrator
   7	Adder Subtractor	Math Block	Add1
   8	Saturation	Non-linear	Saturation
   9	Out-port	Signal Routing	O

   

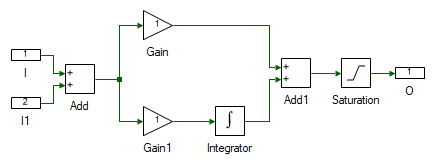
5. Change the properties of each tool to values listed in table below.

   Tool name	Property field	Property value	Comments
   I	Name	Ref	Desired reference motor current.
   I1	Name	Fbk	Actual motor current.
   Add	Arithmetic operation	+-	Difference between the desired and actual motor current.
   Gain	Gain	ki,p	Substitute the value of ki,p computed in step 1.
   Gain1	Gain	ki,i	Substitute the value of ki,i computed in step 1.
   Integrator	Integrator Type	Anti-windup	Reason explained later.
   	Integrator	Upper Limit	38	Set to maximum positive output voltage. This is equal to DC bus voltage minus device drop (≈ 1.5 V).
   	Integrator	Lower Limit	-38	Set to minimum negative output voltage. This is equal to negative of, DC bus voltage minus device drop (≈ 1.5 V).
   Saturation	Upper Limit	38	Set to maximum positive output voltage. This is equal to DC bus voltage minus device drop (≈ 1.5 V).
   	Saturation	Lower Limit	-38	Set to minimum negative output voltage. This is equal to negative of, DC bus voltage minus some device drop (≈ 1.5 V).
   O	Name	Out	Applied terminal voltage to generate the desired current profile.

   When there is a large difference between the desired current and the actual current, the PI controller produces a large output voltage to quickly correct this error. In real-world, the magnitude of this voltage is limited either due to available DC bus voltage or due to motor and power electronics voltage ratings. Hence in practical implementation of PI controller, the output of the PI controller is saturated to the maximum possible voltage. So, during transient conditions, when the actual current is different from the desired current, the Integrator in the PI controller rapidly builds up its output to a large value due to persistent input error. When the error does go back to zero, this large output built up by the integrator does not die down and cause the actual current to overshoot the desired the value, causing the error to go negative, which causes the integrator output to fall, but it will end up falling by much larger value than desired causing the current to undershoot. This keeps repeating, and this oscillation will die down slowly. To avoid this, the value up to which integrator is active is clamped by setting it to Anti-windup. If the integrator output reaches this value, the integrator is disabled until the polarity of the error reverses. This improves the response of the system significantly.

6. Go back to the main motor model by clicking on the tab on the top.

7. Resize the PI controller subsystem so that all the ports can be seen.

8. Add a Step tool and connect the model as shown. Step the current to 1 A at time = 1 s by setting the Final value to 1 and Step time to 1.

   

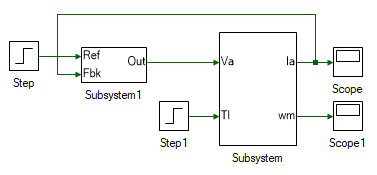
9. Run the simulation and observe the motor current and speed result. Zoom in at time t = 1 s in the current scope to view the step response. As can be seen, the current settles to the Final value within a few milli-seconds compared to speed which takes a few seconds to settle to its Final value. This justifies the earlier assumption in Eqn. 8 where the back-emf was ignored in the small signal model because it changes at much slower rate compared to the current. In most practical motors, the mechanical time constant is orders of magnitude higher than the electrical time constant.

10. Recompute k_i,p and k_i,i for Φ_i,i = π/6 and Φ_i,i = π/2 and obtain the current and speed response for the computed gain values.

Motor speed control

In this section, the speed of the motor is controlled using a PI controller.

1. Compute the k_s,p and k_s,i using Eqn. 14 through 17 for the system to have phase margin Φ_s = π/3 at cross-over frequency ω_s,c = ω_i,i/10 = 2π x 60. The cross-over frequency is chosen as 60 Hz, which is 1/10ᵗʰ the cross-over frequency of inner current loop.

2. Remove the connection between Step tool and the current PI controller subsystem.

3. Copy paste (Ctrl + C, Ctrl + V) the current PI controller subsystem as shown, to add a speed PI control. Connect the tools as shown.

   

   The reference input to this pasted PI controller is the desired motor speed and the feedback is the actual motor speed.

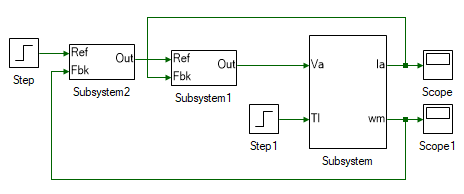
4. The reference speed is stepped to 100 rad/s at time t = 1 s. To do this, change the Final value of Step tool connected to the speed PI controller to 100 and Step time to 1.

5. Change the PI controller gain values in the pasted subsystem to the values computed in step #1.

6. Run the simulation and observe the speed. As can be seen the speed settles rapidly to desired speed in comparison to the open loop system. Also, the speed is maintained even when the load torque was applied. Contrast this with the open loop case where the speed dropped when a load torque was applied.

7. Observe the current result. Based on the motor parameters and the controller gain values used, the current profile will be different. But in most cases (if used with the intended motor), the motor currents would have shot upwards of 5A, which is the maximum current limit of the Three-Inverter box. To prevent this over-current, the output of the integrator and the PI controller needs to be saturated as done for the current PI controller. In the speed PI controller set the Upper Limit to 5 and Lower Limit to -5 for both the Integrator and Saturation tool.

8. Re-run the simulation and observe the result.

   Note

   Both the steady-state motor current and the speed cannot be controlled independently at the same time. The only controllable entity from the user end, within the motor is the applied terminal voltage. Thus, only one motor variable can be controlled in steady-state, i.e. either the motor current, rotor speed or rotor position. When in speed control mode, the inner current loop, merely dictates the path the motor current takes to reach its final steady state. The Final value as such cannot be independently controlled.

Realtime DC motor speed control

In the previous section, the motor speed control model was simulated. In this section, the same system is in run in real-time to control the speed of an actual motor.

1. Open a new Workbench session.

2. Create a new project and add a model file to it. Set this model file as the Start model/Function in project properties.

3. Open model properties and set the Step time to 0.0001 and Run time to 2.

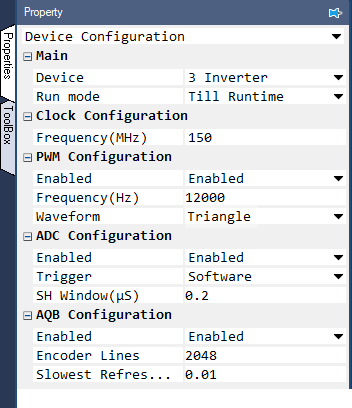
4. Within the project properties, select the drop-down menu on the top and select Device Configuration. Within this, change the following properties:

   1. Change Device within Main sub-division to 3 Inverter

   2. Change Run Mode within Main sub-division to Till Runtime.

   3. Change Frequency (Hz) within PWM Configuration sub-division to 12000.

   4. Change Waveform within PWM Configuration sub-division to Triangle.

   5. Change Encoder Lines within AQB Configuration sub-division to 2048.

   

5. From the simulation model, copy-paste just the speed and current PI controller as shown:

   

6. Drag and drop the following tools from the Toolbox to the model and connect them as shown.

   #	Tool type	Tool class	Tool name
   1	Step	Signal Sources	Step
   2	AQB Speed	Hardware Integration	AQB
   3	Mag-Time Scope	Display	Scope
   4	Analog Input	Hardware Integration	ADC
   5	Gain	Math Block	Gain
   6	Mag-Time Scope	Display	Scope1
   7	Gain	Math Block	Gain1
   8	Constant	Signal Sources	Constant
   9	Adder Subtractor	Math Block	Add
   10	Adder Subtractor	Math Block	Add1
   11	PWM Output	Hardware Integration	PWM
   12	PWM Output	Hardware Integration	PWM1
   13	True/False	Signal Sources	Boolean
   14	Digital Output	Hardware Integration	GPO

   

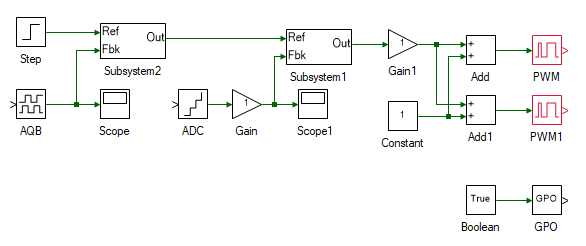
7. Change the properties of each tool to values listed in table below.

   Tool name	Property field	Property value	Comments
   Step	Final value	100	Desired reference motor speed.
   	Step	Step Time	1	Step motor speed from rest to desired speed at time t = 1 s.
   AQB	Channel	1	Actual motor speed feedback.
   ADC	Channel	3	Actual motor current feedback.
   Scope	Realtime log	Enabled	Enable to log real-time motor speed feedback.
   Scope1	Realtime log	Enabled	Enable to log real-time motor current feedback.
   Gain	Gain	-5	Scaling to convert ADC signal to actual current. The scaling value is given within the ADC property.
   Gain1	Gain	1/80	1/(2 x Vdc) to convert the voltage to a value between ±0.5.
   Constant	Magnitude	0.5	Above signal is centered around 0.5 to get the duty cycle.
   Add1	Arithmetic operation	-+	Duty cycle of one of the inverter leg is obtained by adding the scaled duty to 0.5 and other by subtracting it from 0.5.
   PWM	Channel	2	Each PWM channel controls the voltage across one of the output terminals.
   PWM1	Channel	1	Each PWM channel controls the voltage across one of the output terminals.
   Boolean	Value	True	This pulls the inverter out of reset so that it can be used to generate the desired output voltage.
   GPO	Channel	1	Inverter being used is Inverter 1.

8. Connect the motor (the one without the encoder) to Inverter 1 (color of the motor terminal must match that of inverter's). Even though the generator (the one with the encoder) is not used in this case, connected it to Inverter 2 instead of leaving the terminals open.

   Connect the three-inverter module to the DC power supply. Connect the three-inverter to the computer via USB. Connect the generator speed feedback to the three-inverter's Encoder 1 DSUB connector in the back panel.

9. Turn ON the DC power supply and set the voltage to 40 V.

10. Ensure that button on the top dock, to transition to real-time mode, is pressed. Click the run button.

11. Observe the speed and current result in the scope. Click the to focus the result. After about 2 s, stop data logging by clicking .

12. Turn OFF the DC power supply.

13. In some cases, the current may be extremely choppy. This happens due to the speed controller trying to correct the noise in the speed feedback in real-time mode. To avoid this, redesign the PI controller for cross-over frequency of 6 Hz, i.e. ω_s,c = ω_i,i/100 = 2π x 6.

    Use the redesigned PI values and re-run the motor.

14. Replace the Step reference by a Sine reference of Magnitude equals 100 and Frequency equals 1.

15. Turn ON the DC power supply and re-run the model.

16. Observe if the motor tracks the reference speed.

17. Turn OFF the DC power supply and disconnect all the connections including the USB.

This concludes the experiment on DC motor speed control. In this experiment, the DC motor was actively loaded only in simulation and not in real-time. This will be done in the following experiment, where controller designed in this experiment will be used.

Lab report and reading assignment

1. Attach plot of I_a and ω_m from simulation when motor was operated in open loop.

2. Mention the PI controller gain values obtained. Attach plot of I_a and ω_m from simulation when motor was operated in current control mode, for different gain values.

3. Mention the PI controller gain values obtained. Attach plot of I_a and ω_m from simulation when motor was operated in speed control mode.

4. Attach plot of ω_m from real-time speed control.

5. In current control mode what would the speed profile look like if frictional coefficient, B was zero and there is no voltage limitation?

6. How will you extend the speed control model to do position control? What will be system transfer function that will be used to tune the PI controller?